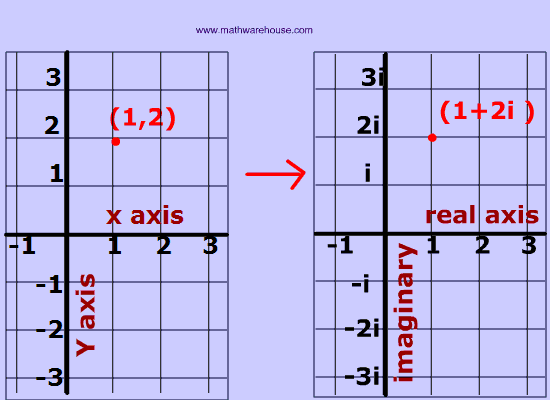
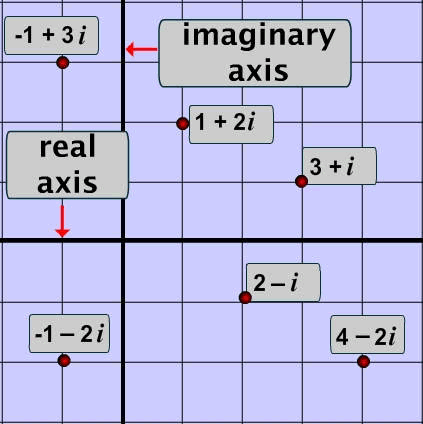
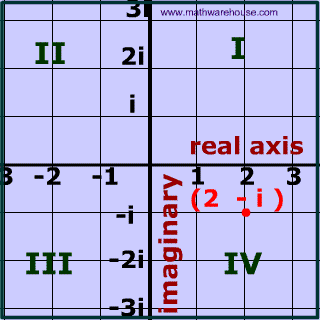
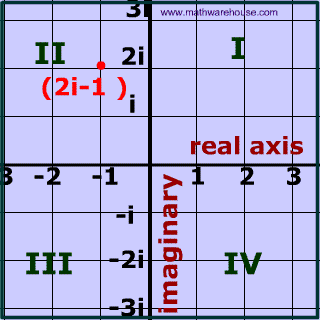
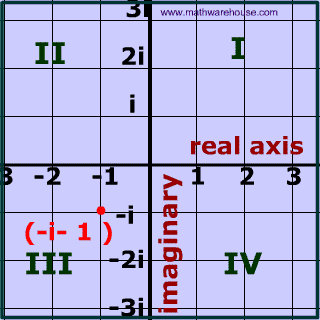
A complex number can be written in the form a + b
i where a and b are real numbers (including 0) and
i is the
imaginary number i. Therefore a complex number contains two 'parts'; one that is real, and another part that is imaginary.
How to Graph
Complex numbers are often represented on a complex number plane (which looks very similar to a cartesian plane). On this plane, the imaginary part of the complex number is measured by the vertical axis (on the cartesian plane, this is the y axis) and the real number part of goes on the horizontal axis (where the 'x' values of coordinates normally go).
