Video Tutorial
How to write sohcahtoa ratios, given side lengths
Practice writing the ratios
How to write sohcahtoa ratios, given side lengths
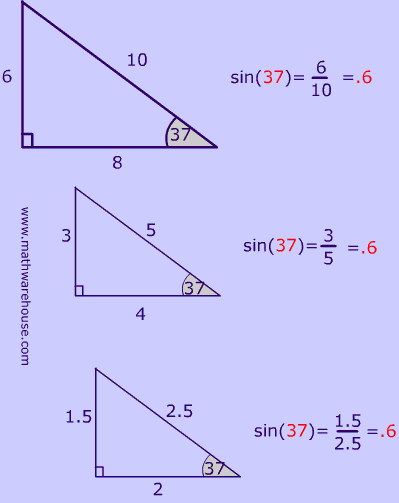
Sine, cosine and tangent of an angle represent the ratios that are always true for given angles. Remember these ratios only apply to right triangles.
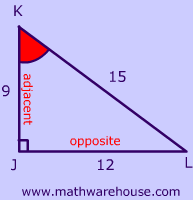
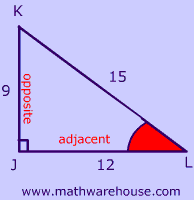
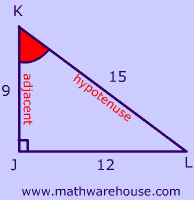
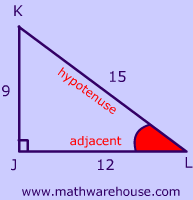
The 3 triangles pictured below illustrate this.
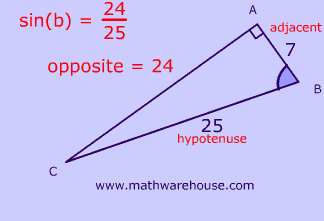
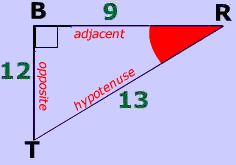
Although the side lengths are different , each one has a 37° angle, and as you can see, the sine of 37 is always the same!
In other words, $$sin(\red { 37^{\circ} } )$$ is always $$ \red {.6 } $$ .
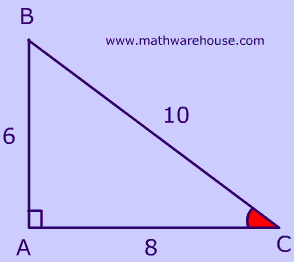
In the diagram 2, what side is adjacent to $$\angle L$$?
$$ \overline{ML} $$.
What side is the hypotenuse?
$$ \overline{ LN} $$
Calculate $$cos(\angle L)$$.
Use sochcahtoa to help remember the ratio.
$ cos(\angle \red L) = \frac{adjacent}{hypot} \\ cos(\angle \red L) = \frac{8}{10} \\ = .8 $
Calculate $$ cos(\angle N)$$ (a different angle from prior question, look carefully at letters).
$ cos(\angle \red N) = \frac{6}{10} \\ = .6 $
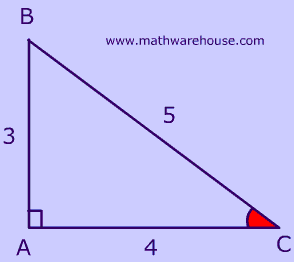
What is the sine ratio of $$\angle C$$ ?
Remember the sine ratio
$ sin(\angle C) =\frac{\text{opp } }{ hypot} \\ sin(\angle C) = \frac{6}{10} \\ sin(\angle C) = \frac{6}{10} \\ sin(\angle C) = .6 $
What is the cosine ratio of $$\angle C $$ in $$ \triangle ABC$$ ?
Remember the cosine ratio
$ cos(\angle C) =\frac{\text{adj } }{ hypot} \\ cos(C) = \frac{4}{5} \\ cos(C) = .8 $
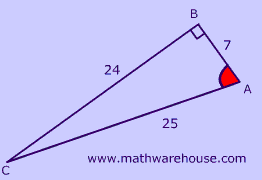
What is the tangent ratio of $$\angle A$$ ?
Use sochcahtoa to help remember the ratio.
$ tan(A) = \frac{opposite}{adjacent} \\ = \frac{24}{7} \\= 3.42857142 $
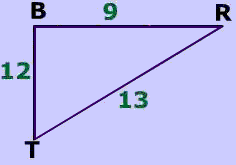
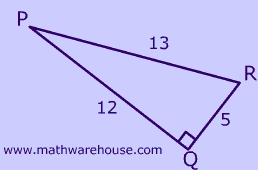
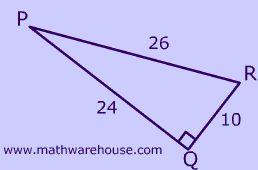
Find the sine, cosine and tangent of $$\angle R$$.
Use sochcahtoa to help remember the ratios.
$$ \text{ for } \angle \red R \\ \boxed { Sine } \\ sin(\red R )= \frac{opp}{hyp} \\ sin(\red R )= \frac{12}{13} \\ sin(\red R )= .923 \\ \boxed{ cosine } \\ cos(\red R)= \frac{adj}{hyp} \\ cos(\red R)= \frac{9}{13} = \\ cos(\red R).69 \\ \boxed{ tangent } \\ tan(\red R)= \frac{opp}{adj} \\ tan(\red R) = \frac{12}{9} \\ tan(\red R)= 1.3 $$
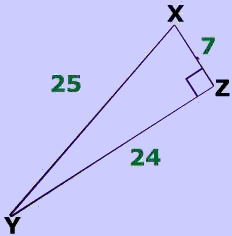
What is $$sin(\angle X)$$?
$$ sin(\red X ) = \frac{opp}{hyp} \\ sin(\red X ) = \frac{24}{25} \\ sin(\red X ) = .96 $$
What is $$cos(\angle X)$$?
$$ sin(\red X) = \frac{adj}{hyp} \\ sin(\red X) = \frac{7}{25} \\ sin(\red X) = .28 $$
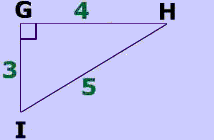
Calculate : $$\text{ a) } sin(\angle H) \\ \text{ b) }cos(\angle H) \\ \text{ c) } tan(\angle H)$$
$$ sin(\angle \red H) = \frac{3}{5} \\ sin( \angle \red H) = .6 \\ cos(\angle \red H) =\frac{ 4}{5} \\ cos (\angle \red H)= .8 \\ tan(\angle \red H) = \frac{3}{4} \\ tan(\angle \red H)= .75 $$
Which angle below has a tangent ratio of $$\frac{3}{4}$$?
Use sochcahtoa to help remember the ratio for tangent.
$$ tangent = \frac{opp}{adj} $$
So which angle has a tangent that is equivalent to $$\frac{3}{4}$$?
You only have 2 options. Either $$\angle L$$ or $$ \angle K $$. So let's calculate the tangent for each angle.
$ tan( \angle K) = \frac{12}{9} \\ \frac{12}{9} \red {\ne} \frac 3 4 $
$ tan( \angle L) = \frac{9}{12} \\ \frac{9}{12} = \frac 3 4 $
Which angle below has a cosine of $$\frac{3}{5}$$?
Use sochcahtoa to help remember the ratio for tangent.
$$ cosine = \frac{adj}{hyp} $$
So which angle has a cosine that is equivalent to $$\frac 3 5 $$?
You only have 2 options. Either $$\angle L$$ or $$ \angle K $$. So let's calculate the tangent for each angle.
$ cos( \angle K) = \frac{9}{15} \\ \frac{9}{15} \red {\ne} \frac 3 4 $
$ cos(L) = \frac{12}{15} \\ \frac{12}{15} = \frac 3 5 $
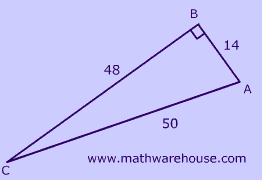
Which angle below has a tangent $$\approx$$ .29167?
This is a little trickier because you are given the ratio as a decimal; however, you only have two options. Either $$ \angle A $$ or $$\angle C $$.
$$ tan(\angle A) = \frac{48}{14} \\ tan(\angle A)= 3.42857 $$
$$ tan(\angle C) = \frac{14}{48} \\ tan(\angle C) = .29167 $$
Which angle below has a tangent of 2.4?
Again, there are two options (angles R or P), but since your ratio is greater than 1 you might quickly be able to notice that it must be R.
$$ tan(\angle P) = \frac{5}{12} \\ tan(\angle P) = 0. 41666 $$
$$ tan(\angle R) = \frac{12}{5} \\ tan(\angle R) = 2.4 $$
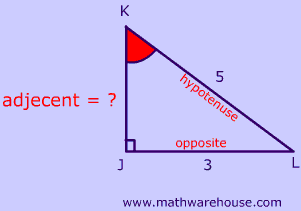
It's easiest to do a word problem like this one, by first drawing the triangle and labelling the sides. We know the opposite side of $$ \angle K$$ and we know the hypotenuse.
To get the tangent ratio we need to know the length of the adjacent side.
How can we find the length of the adjacent side?
Use the Pythagorean theorem!
$$ a^2 + b^2 = c^2 \\ 3^2 + b^2 = 5^2 \\ b^2 = 5^2- 3^2 = 25-9 = 16 \\ b = 4 $$
Now, use the tangent ratio!
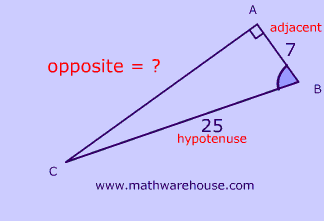
Draw this triangle and label the sides:
Remember that the cosine ratio = $$\frac{adjacent}{hypotenuse}$$.
How can we find the length of the opposite side?
(Remember that sine involves the opposite so we need to find that somehow).
Use the Pythagorean theorem!
$$ a^2 + b^2 = c^2 \\ 7^2 + b^2 = 25^2 \\ b^2 = 25^2- 7^2 = 625 - 49 = 576 \\ b = \sqrt{576} =24 $$
Now, use the sine ratio!
$$ sin(b) = \frac{opposite}{hypotenuse} $$
Be careful!
In the triangle below, which angle has a sine ratio of 2.6?
There is no angle that has a sine of 2.6.
Remember that the maximum value of the sine ratio is 1.
The same, is true, by the way of cosine ratio (max value is 1).