Inverse SOHCAHTOA Way vs Interior Angle Sum
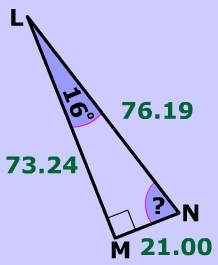
Compare This Method To the tried and true theorem that the sum of the interior angles of a triangle is 180°.
What is the degree measure of
![]() LNM?
LNM?
Since the total measure of the interior angles of a triangle is 180 degrees we can verify the measure of
![]() LNM:
LNM:
![]() 180° -16° - 90° =74 °
180° -16° - 90° =74 °
Alternately, you could use the inverse of one of the SOHCAHTOA functions, in this case the inverse of sine (sin-1)! To find, an angle of a right triangle all that we need to know is the length of two sides! Then use the same SOHCAHTOA ratios -- just in a different fashion See the example below.

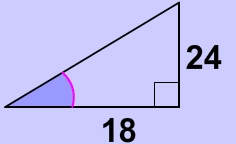
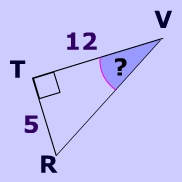
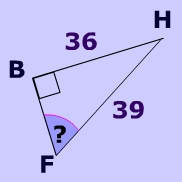
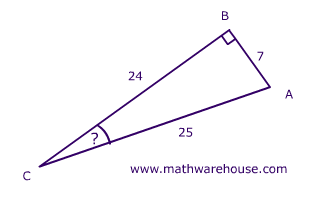
 in the triangle below?
in the triangle below? 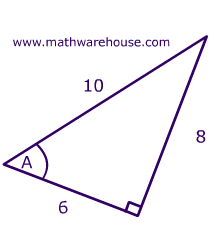
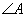 in the triangle below. Round
in the triangle below. Round 










