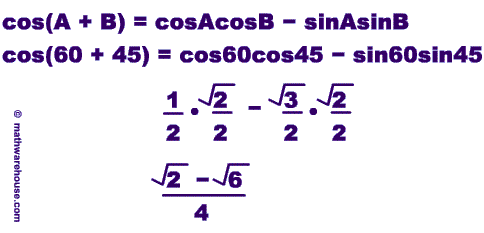The angle sum identities take two different formulas:
- sin(A+B) = sinAcosB + cosAsinB
- cos(A+B) = cosAcosB − sinAsinB
These formulas allow you to express the exact value of trigonometric expressions that you could not otherwise express. Consider the sin(105°). Unlike the sin(30) which can be expressed as ½, the sin(105) cannot simply be represented as a rational expression. However, the angle sum formula allows you to represent the exact value of this function
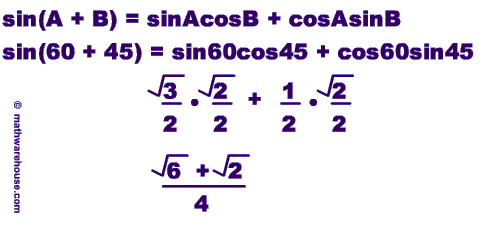
Since 75° = 30° + 45° we can use our formula to rewrite cos(75) as cos(30° + 45°)
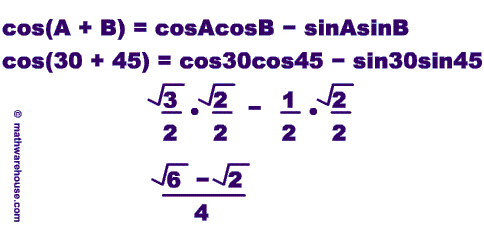
Since 75° = 30° + 45° we can use our formula to rewrite sin(75) as sin(30° + 45°)
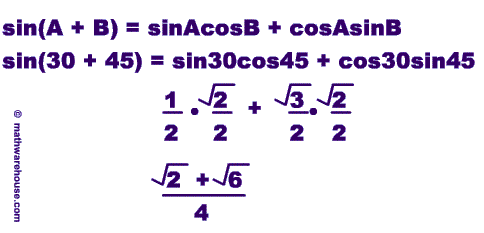
Since 105° = 60° + 45° we can use our formula to rewrite cos(105) as cos(60° + 45°)