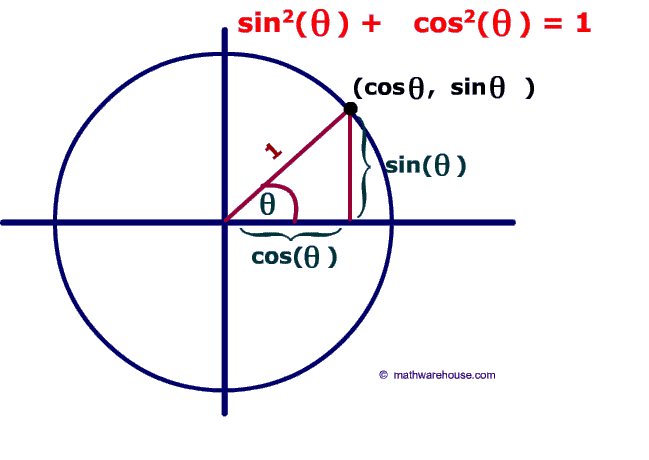The picture shows a point on the unit circle. Since we know that any point on the unit circle can be described by $$cosθ$$ , $$sinθ$$. It is possible to draw the triangle that describes this formula. As you can see from the picture below, the length of one side is cosθ and the length of the other side is sinθ and, by definition, the radius of the unit circle is 1. From these facts, the primary Pythagorean identity can be shown. sin2θ + cos2θ = 1. This identity is just an application of the Pythagorean theorem to the unit circle.
Formula for the Pythagorean Identities
- $$ sin^2 \theta $ ; + cos^2 \theta = 1$$
- $$ tan^2 \theta + 1 = sec^2 \theta $$
- $$ 1 + cot ^2 \theta = csc^2 \theta $$
Pictured below is the formula for the aptly named Pythagorean identity:
$$sin^2 \theta + cos^2 \theta = 1$$