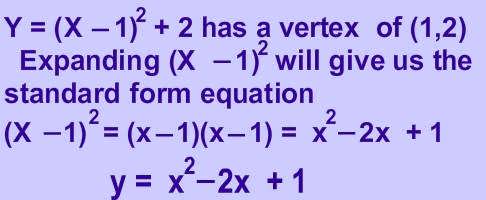Standard Form Equation
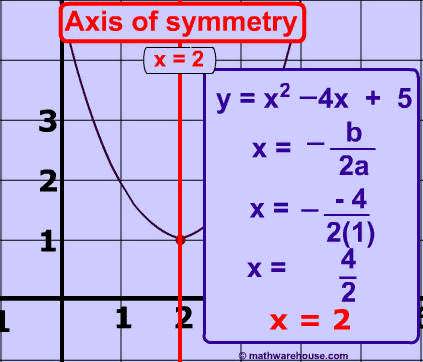
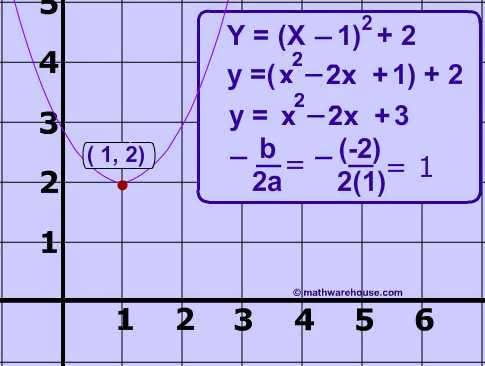
The standard form of a parabola's equation is generally expressed:
$ y = ax^2 + bx + c $
The role of a in $$ {\color{Red}a}x^2 + bx + c $$
| $$ a > 0 $$ |
parabola's opens upwards like a 'U' 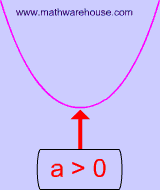
|
| $$ a < 0 $$ |
parabolas opens downwards like an upside down 'U' 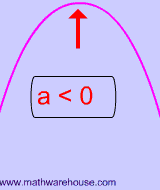
|
- If $$|a| < 1 $$, the graph of the parabola's widens. This just means that the "U" shape of parabola stretches out sideways .
- If $$ |a| > 1 $$, the graph of the graph becomes narrower(The effect is the opposite of |a| < 1).