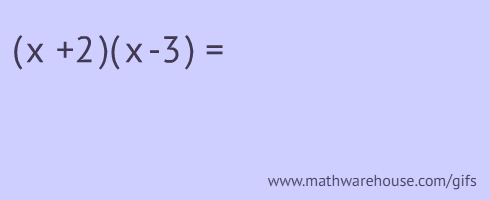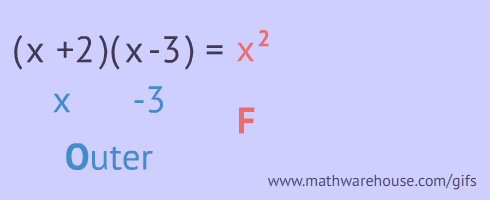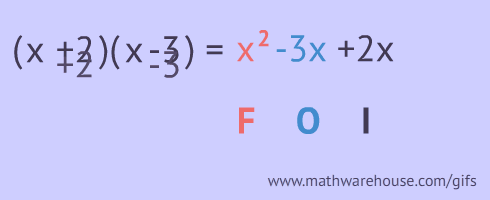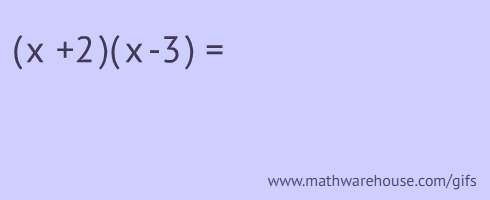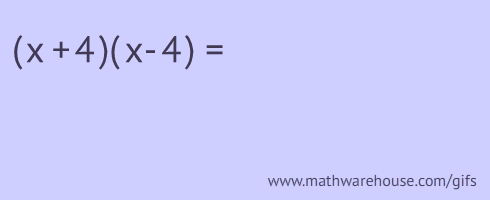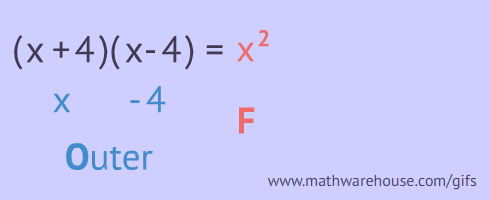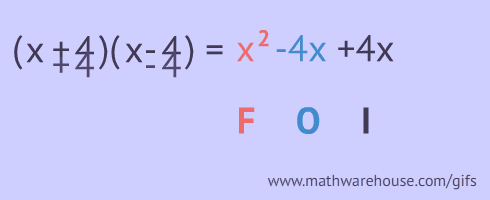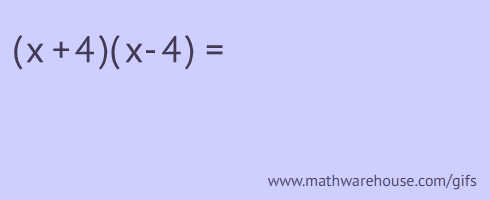Mathwarehouse Logo
foil method animated gif

Examples and practice with formula

What "FOIL" stands for

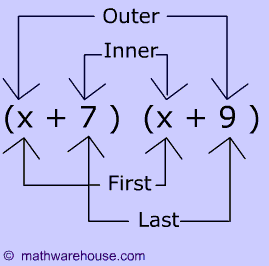
"Foil" is a way that people remember the 'formula' for multiplying binomials. (An alternative approach is to use "a href="/properties/double-distributive-property.php">double distributive").

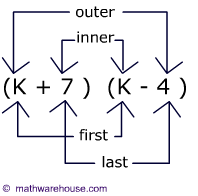
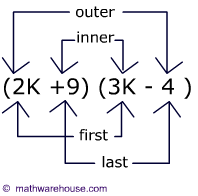
FOIL stands for first, outer, inner and last pairs. You are supposed to multiply these pairs as shown below!

Firsts:
$$ x \cdot x= x^2 $$
Outers:
$$ x \cdot 9 =9x $$
Inners:
$$ 7 \cdot x =7x$$
Lasts:
$$ 7 \cdot 9 = 63$$
FOIL explained binomials

So, now that we've multiplied, what is next?

Add up each term!

$$ x^2 $$
$$9x$$
$$7x$$
$$+ 63$$
$$ x^2 + 16x + 63 $$

Video Multiplying Binomials

Visualizing with Rectangles and Area

What is the area of the rectangle below?

Foil as area of rectangles

The area of each part of the rectangle can be seen as a 'part' of the FOIL formula.

Example 1

Let's multiply the following binomials: (X + 3)(X + 2).

Step 1
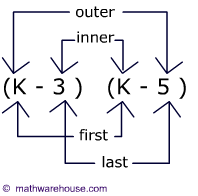
Picture of Foil Method

First: x • x = $$ x^2 $$
Outer: x • 2 = 2x
Inner: 3 • x = 3x
Last: 3 • 2 = 6

Practice Problems

Problem 1

Multiply the 2 binomials: $$(k + 7)(k - 4) $$.

Step 1

This is like example 1.

Picture of Foil Method

First: k • k = k²
Outer: k • -4 = -4k
Inner: 7 • k = 7k
Last: 7 • -4 = -28

Step 2

Simplify by adding the terms.

$$ k^2 $$
-4k
7k
+ (-28)
k2+ 3k - 28
Problem 2

Multiply the following binomials: $$(k - 3)(k - 5) $$.

Step 1

This is like example 1.

Multiply the first, outer, inner and last pairs.

Picture of Foil Method

First: k • k = k²
Outer: k • -5 = -5k
Inner: -3 • k = -3k
Last: -3 • -5 = 15

Step 2

Simplify by adding the terms.

k²
-5k
-3k
+ 15
k2 − 8k + 15
Problem 3

Multiply the binomials: $$ (2k + 9)(3k - 4) $$.

Step 1

This is like example 1. with the slight twist that you now have to deal with coefficients in from of the variable of each binomial.

Multiply the first, outer, inner and last pairs.

Picture of Foil Method

First: 2k • 3k = 6k²
Outer: 2k • -4 = -8k
Inner: 9 • 3 k = 27k
Last: 9 • -4 = -36

Step 2

Simplify by adding the terms.

6k²
-8k
27k
+ (-36)
6k2+ 19k + -36
Problem 4

Multiply the 2 binomial:below: $$ (5k - 1)(2k + 3) $$.

Step 1

This is like example 1 with the slight twist that you now have to deal with coefficients in form of the variable of each binomial.

Multiply the first, outer, inner and last pairs.

Picture of Foil Method

First: 5k • 2k = 10k²
Outer: 5k • 3 = 15k
Inner: -1 • 2k = -2k
Last: -1 • 3 = -3

Step 2

Simplify by adding the terms.

10k²
15k
-2k
+ (-3)
10k2+ 13k + -3
Multiply Binomials Calculator (Enter the binomials, and we'll do the work)
Multiplying Binomials - Double Distributive Method
Multiplying Binomials Worksheet
Further Reading:
Back to Multiplying Polynomials Next to Special Binomials

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!