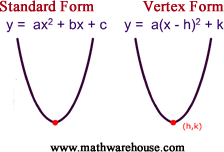
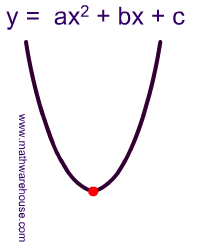
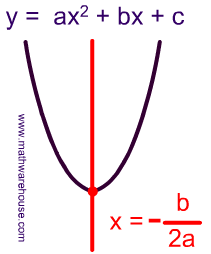
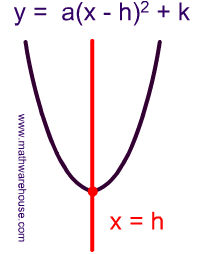
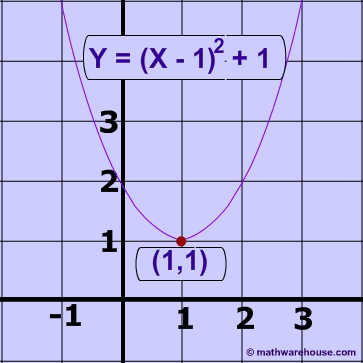
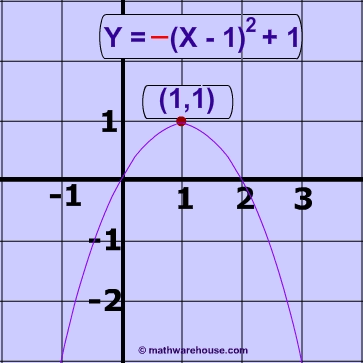
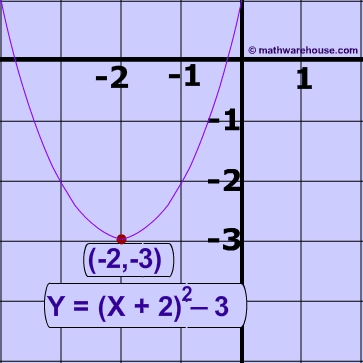
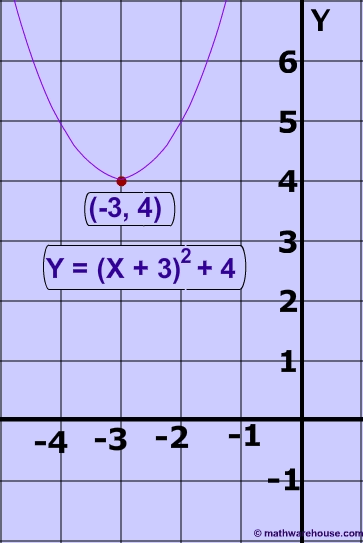
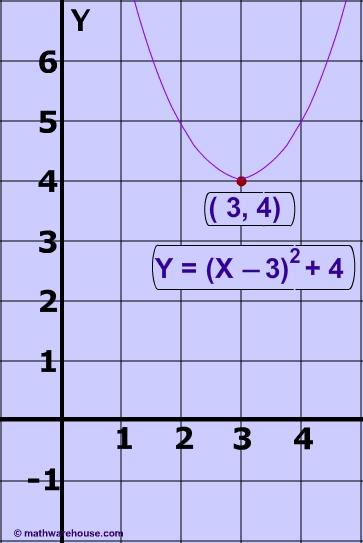
The vertex form of a parabola's equation is generally expressed as: $ y = a(x-h)^2 +k $
- (h,k) is the vertex as you can see in the picture below
![parabola opens upwards or downards]()
![Vertex Form Axis]()
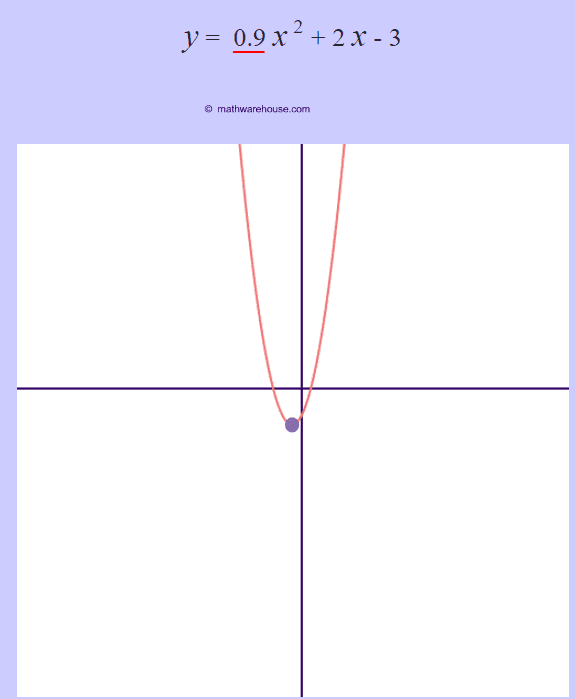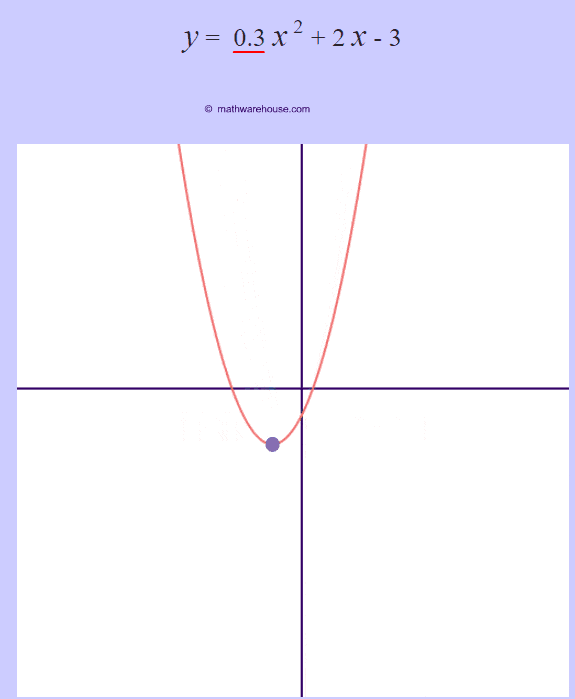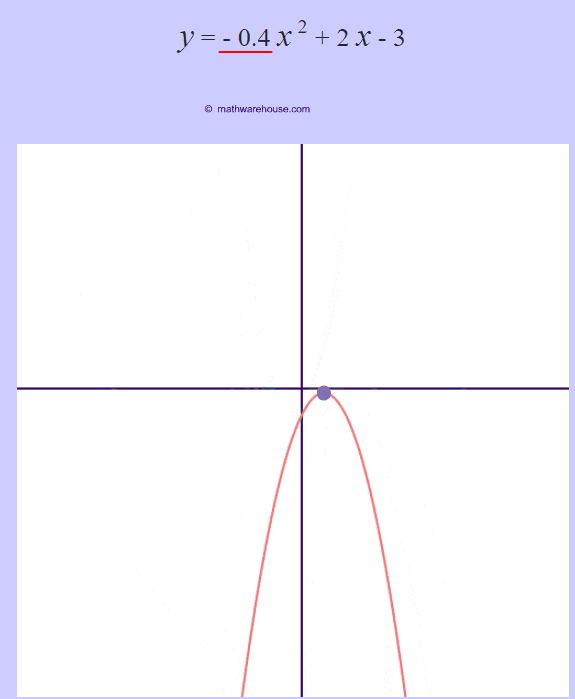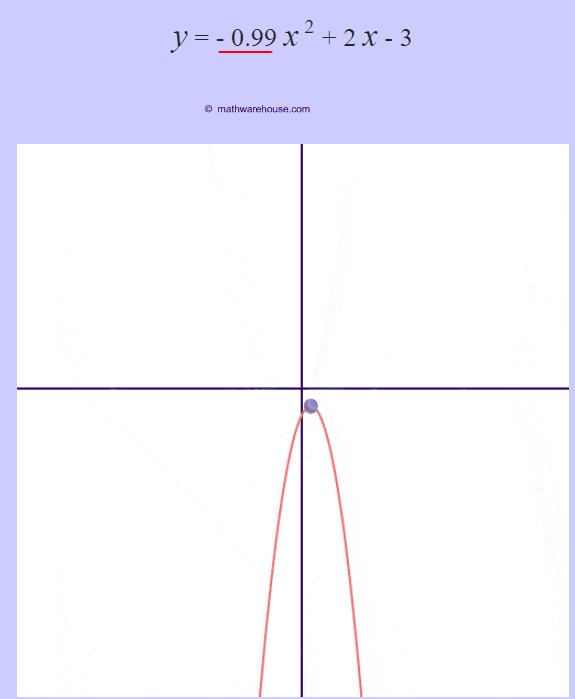
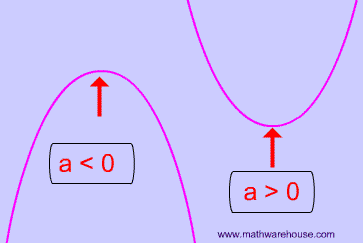
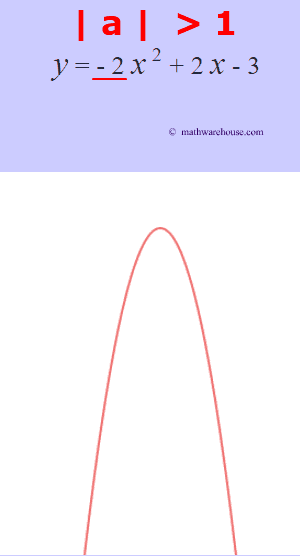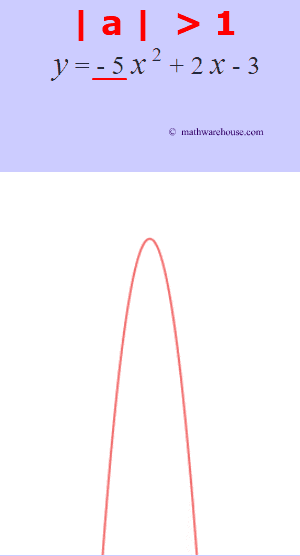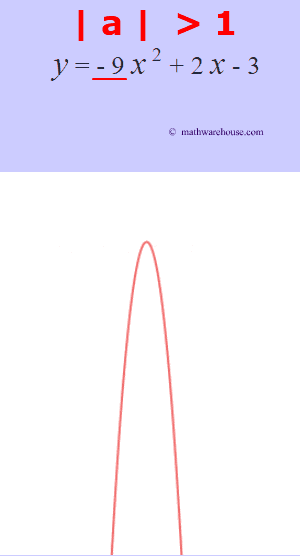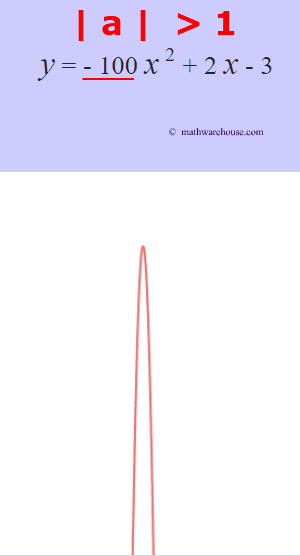
- If a is positive then the parabola opens upwards like a regular "U".
- If a is negative, then the graph opens downwards like an upside down "U".
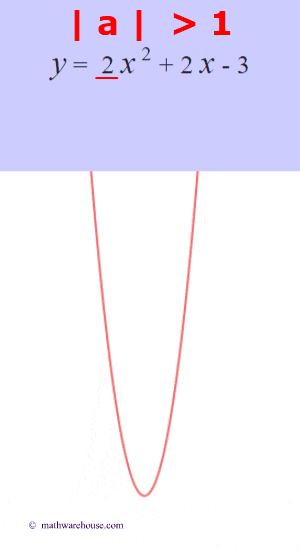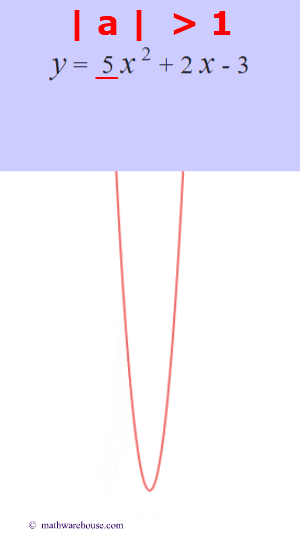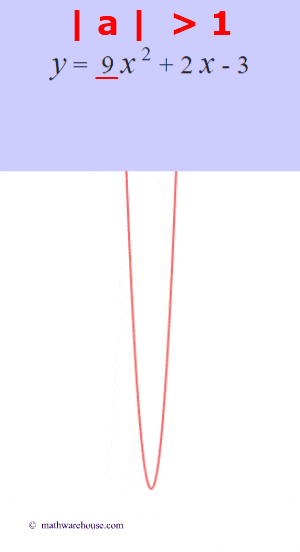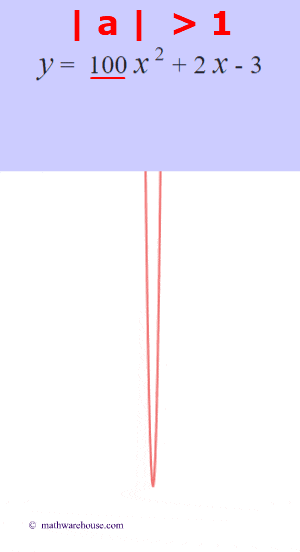
- And, just like standard form, the larger the $ |a|$, the more narrow the parabola's graph gets.
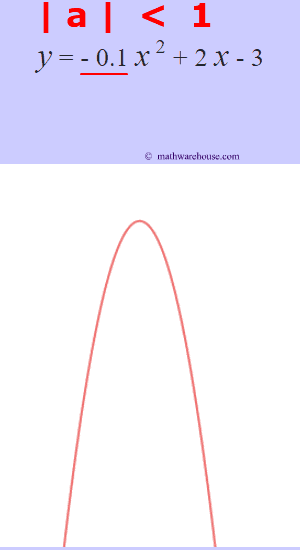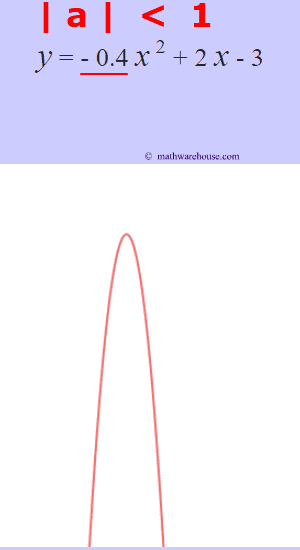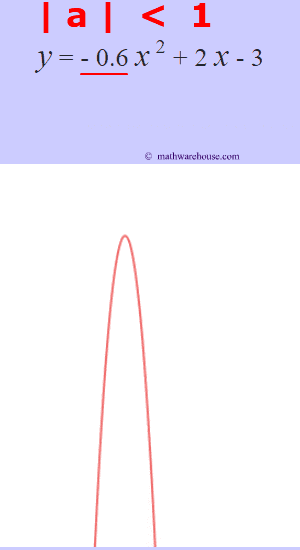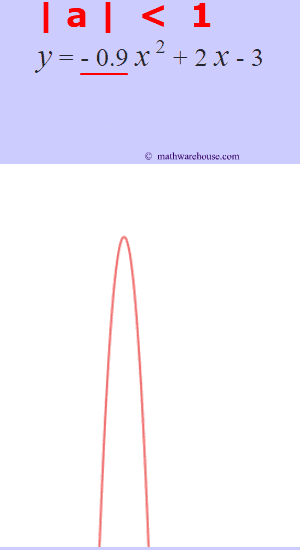
The role of 'a'
The larger the $ |a|$ is, the more the graphs narrows.
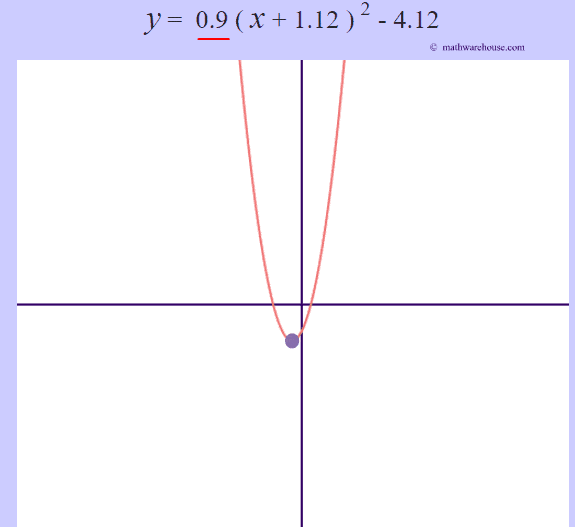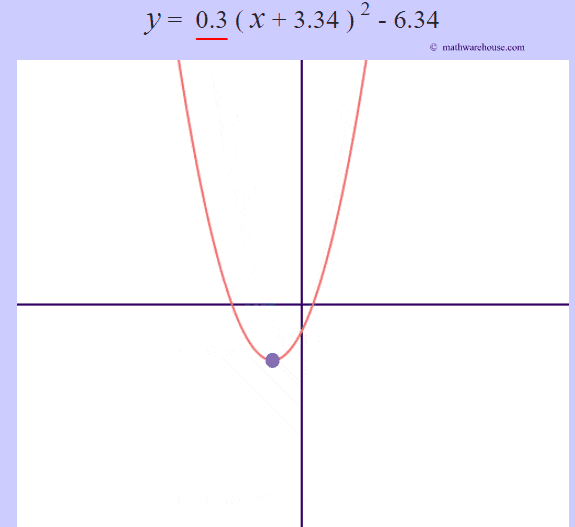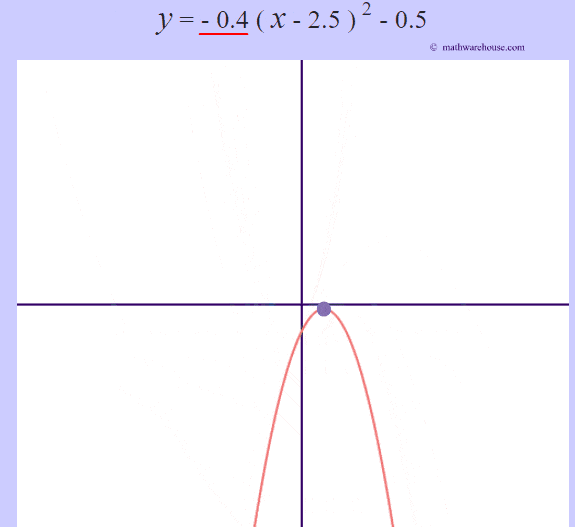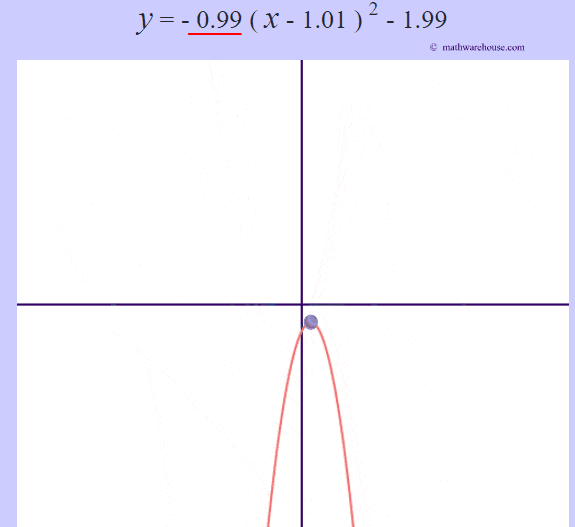
The larger the $ |a|$ is, the more narrow the parabola is. Or, another way to think of it, the closer that the value of $a$ gets to zero, the wider the parabola becomes.