Real World applications of Parabolas. Several practice problems with pictures and answers

Problem 1

Below is a picture of a rainbow that makes a perfect parabola. What is the vertex of the parabola?

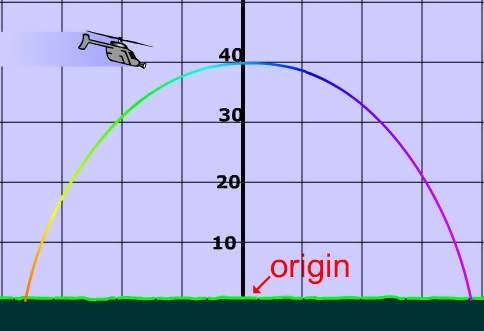
Vertex of parabola is (0,40)

For the helicopter to fly above the rainbow parabola, how high must the copter fly? (In other words what is the maximum value of the parabola)

The helicopter must be above 40.

This real is simply a real world application of how to find the vertex of a parabola

Problem 2

Joseph threw a whiffle ball out of a window that is four units high. The position of the waffle ball is determined by the parabola y = -x² + 4. At how many feet from the building does the ball hit the ground?

The ball lands at the solution of this quadratic equation. There are two solutions. One at 2 and the other at − 2. This picture assumes that Joseph threw the ball to the right so that the whiffle balls lands at 2

You can solve this quadratic by factoring or by using the quadratic formula

Problem 3

Down in the street, Eric caught the ball and then he ran to 10 feet away from the base of the building. Eric throws the ball so that its highest point is where the x is on the first floor. What equation represents the path of the ball that Eric threw?

Problem 4

A ball is dropped from a height of 36 feet. The quadratic equation d = -t² + 36 provides the distance, d, of the ball, after t seconds. After how many seconds, does the ball hit the ground?

The ball hits the ground at d = 0. To find the value of t at this point we must solve this quadratic equation.

0 = −t² + 36
t² = 36
t = 6

(Note: t = -6 is also a solution of this equation. However, only the positive solution is valid since we are measuring seconds.)

Problem 5

A ball is dropped from a height of 60 feet. The quadratic equation d = −5t² + 60 provides the distance, d, of the ball, after t seconds. After how many seconds, does the ball hit the ground?

We want to find when d=0, which represents the moment when the ball hits the ground.

d = 0, when 0 = -5t² +60
5t² = 60
t² = 60 ÷5 = 12

$$ \sqrt{12} \approx 3.5 $$

Problem 6

The height in meters of a projectile at t seconds can be found by the function $$ h(t) = -5t^2 + 40t + 1.2 $$.

Find the height of the projectile 4 seconds after it is launched.

Step 1

Identify all of the occurrences of 't' and substitute the input in

$$ h( {\color{blue} t} ) = -5 {\color{blue} t} ^2 + 41 {\color{blue}t} + 1.2 \\ h( {\color{blue}4} ) = -5 \cdot {\color{blue}4}^2 + 40 \cdot {\color{blue} 4} + 1.2 $$

Step 2

Compute result

$$ h( {\color{blue} 4}) = -5 \cdot {\color{blue} 4}^2 + 40 \cdot {\color{blue} 4} + 1.2 \\ h( {\color{blue} 4}) = {\color{red} 81.2} $$

Step 3

$$ h({\color{blue} input}) = {\color{red} output} \\ h({\color{blue} 4} ) = {\color{red} 81.2} $$

Here is a picture of graph of projectile's path with the point $$ ({\color{blue} t}, {\color{red} h(t)}) ({\color{blue} 4}, {\color{red} 81.2}) $$