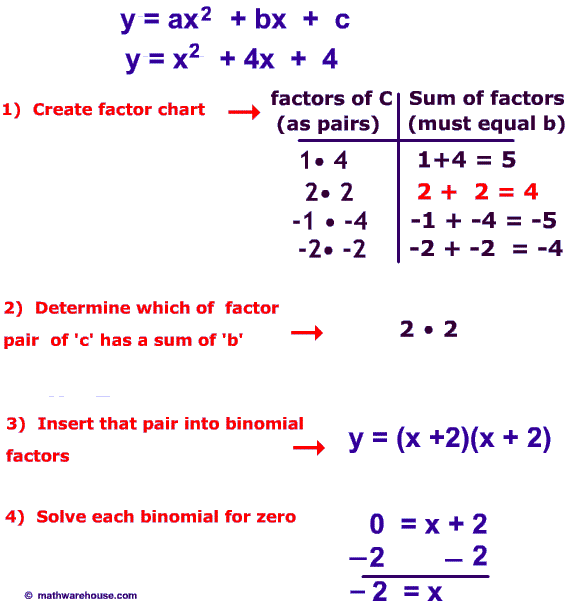What is a Quadratic Equation?
A quadratic equation is an equation that can be written as:
$$ ax^2 + bx + c $$ where a ≠ 0.
A quadratic equation must have a squared term as its highest power.
Step by Step Examples
A quadratic equation is an equation that can be written as:
$$ ax^2 + bx + c $$ where a ≠ 0.
A quadratic equation must have a squared term as its highest power.
$$ y = 5x^2 + 2x + 5 \\ y = 11x^2 + 22 \\ y = x^2 - 4x +5 \\ y = -x^2 + 5 $$
$$ y = 11x + 22 \\ y = x^3 -x^2 +5x +5 \\ y = 2x^3 -4x^2 \\ y = -x^4 + 5 $$
The solution of a quadratic equation is the value of x when you set the equation equal to $$ \red {\text {zero}}$$
i.e. When you solve the following general equation: $$\red 0 = ax^2 + bx + c $$.
There are many ways to solve quadratic equations. One of the ways is to factor the equation.
Create a factor chart for all factor pairs of c.
A factor pair is just two numbers that multiply and give you c.
Note: if the pair does not exist, you must either complete the square or use the quadratic formula.
Solve each binomial for zero to get the solutions of the quadratic equation.
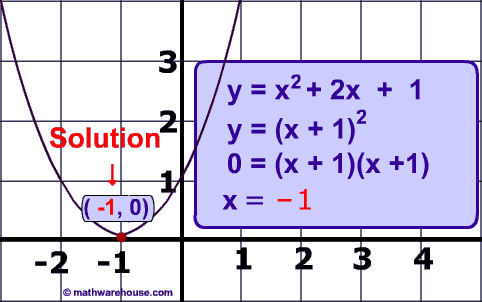
Quadratic Equation: y = x² + 2x + 1.
Below is a picture representing the graph of y = x² + 2x + 1 as well as the solution we found by factoring.
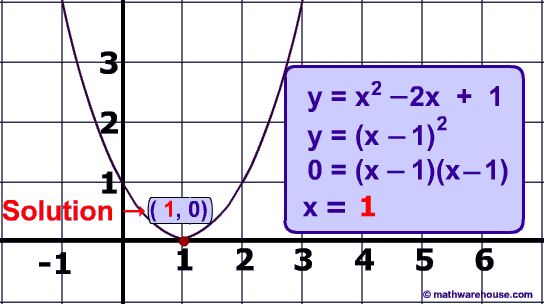
Below is a picture of the graph of the quadratic $$ y = x^2 - 2x + 1 $$as well as the solutions.
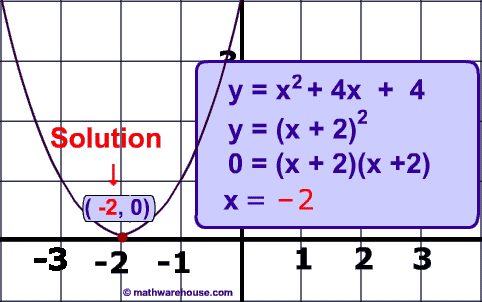
Below is a picture of the graph of the quadratic $$ y = x^2 + 4x + 4 $$ as well as the solutions.
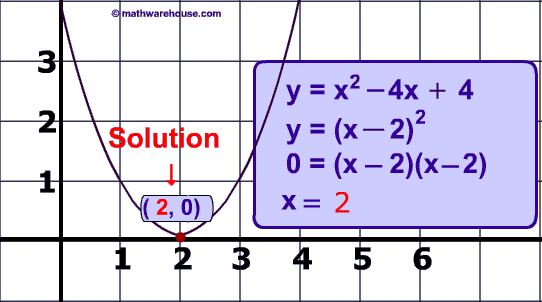
$$ y = x^2 - 4x + 4 $$ is graphed below as well as its solution (2, 0).
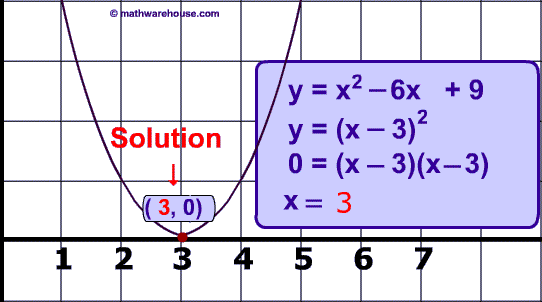
$$ y = x^2 + 6x + 9 $$ is graphed below as well as its solution (2, 0).
y = x² − 6x + 9
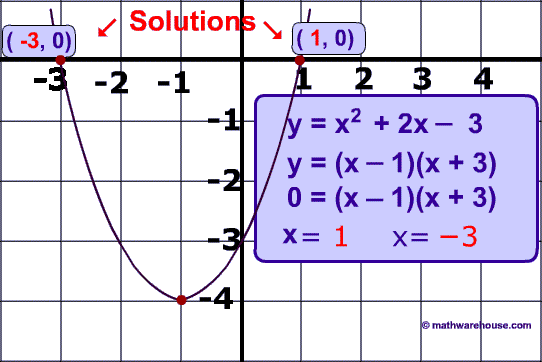
$$ y = x^2 + 2x - 3$$ is graphed below as well as both the solutions.
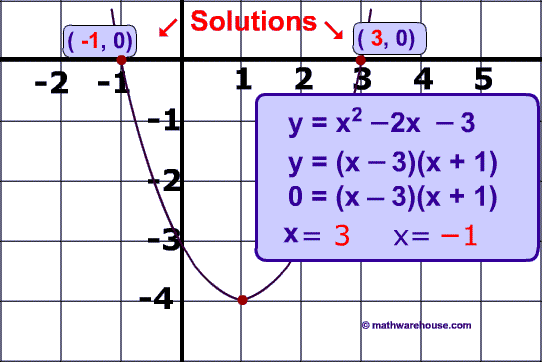
$$ y = x^2 - 2x - 3 $$ is graphed below as well as both the solutions.