Quick Overview
- Discontinuities can be classified as jump, infinite, removable, endpoint, or mixed.
- Removable discontinuities are characterized by the fact that the limit exists.
- Removable discontinuities can be "fixed" by re-defining the function.
- The other types of discontinuities are characterized by the fact that the limit does not exist. Specifically,
- Jump Discontinuities: both one-sided limits exist, but have different values.
- Infinite Discontinuities: both one-sided limits are infinite.
- Endpoint Discontinuities: only one of the one-sided limits exists.
- Mixed: at least one of the one-sided limits does not exist.
Jump Discontinuities
The graph of $$f(x)$$ below shows a function that is discontinuous at $$x = a$$.
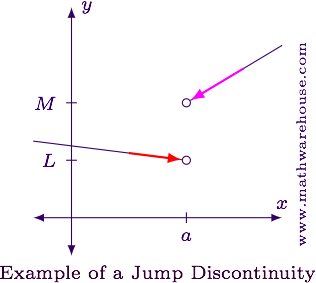
In this graph, you can easily see that $$ {\color{importantColor}\lim\limits_{x\to a^-} f(x) = L} % \mbox{ and } % {\color{secondaryColor}\lim\limits_{x\to a^+} f(x) = M}. $$
The function is approaching different values depending on the direction $$x$$ is coming from. When this happens, we say the function has a jump discontinuity at $$x=a$$.
Infinite Discontinuities
The graph below shows a function that is discontinuous at $$x=a$$.
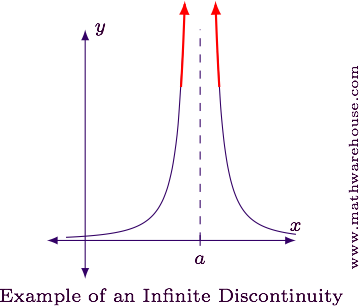
The arrows on the function indicate it will grow infinitely large as $$x$$ approaches $$a$$. Since the function doesn't approach a particular finite value, the limit does not exist. This is an infinite discontinuity.
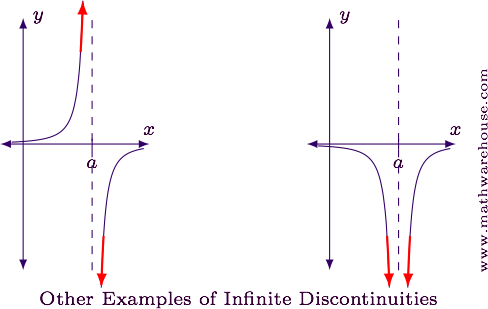
The following two graphs are also examples of infinite discontinuities at $$x = a$$. Notice that in all three cases, both of the one-sided limits are infinite.
Removable Discontinuities
In the graphs below, there is a hole in the function at $$x=a$$. These holes are called removable discontinuities
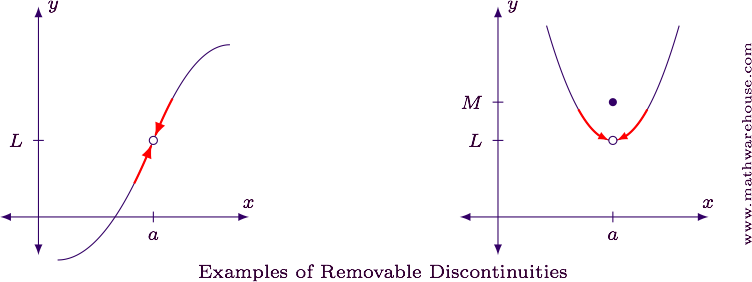
Notice that for both graphs, even though there are holes at $$x = a$$, the limit value at $$x=a$$ exists.
Removable Discontinuities can be Fixed
Removable discontinuities can be fixed by redefining the function, as shown in the following example.
Example
The function below has a removable discontinuity at $$x = 2$$. Redefine the function so that it becomes continuous at $$x=2$$.
$$f(x) = \frac{x^2-2x}{x^2-4}$$
SolutionThe graph of the function is shown below for reference.
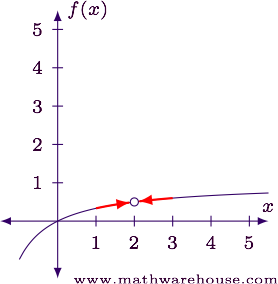
In order to fix the discontinuity, we need to know the $$y$$-value of the hole in the graph. To determine this, we find the value of $$\lim\limits_{x\to 2} f(x)$$.
Examining the form of the limit we see
$$\displaystyle\lim_{x\to 2} \frac{x^2-2x}{x^2-4} = \frac{(2)^2 - 2(2)}{(2)^2-4} = \frac 0 0$$
The division by zero in the $$\frac 0 0$$ form tells us there is definitely a discontinuity at this point.
Next, using the techniques covered in previous lessons (see Indeterminate Limits---Factorable) we can easily determine
$$\displaystyle\lim_{x\to 2} f(x) = \frac 1 2$$
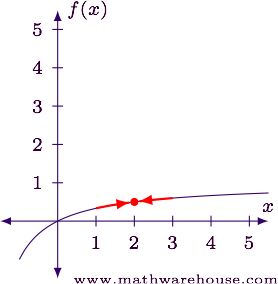
The limit value is also the $$y$$-value of the hole in the graph. Now we can redefine the original function in a piecewise form:
$$ \\ f(x) = \left\{% \begin{array}{ll} \frac{x^2-2x}{x^2-4}, & \mbox{for all } x \neq 2\\[6pt] % \frac 1 2, & \mbox{for } x = 2 \end{array} \right. \\ $$
The first piece preserves the overall behavior of the function, while the second piece plugs the hole.
Endpoint Discontinuities
When a function is defined on an interval with a closed endpoint, the limit cannot exist at that endpoint. This is because the limit has to examine the function values as $$x$$ approaches from both sides.
For example, consider finding $$\displaystyle\lim\limits_{x\to0} \sqrt x$$ (see the graph below).
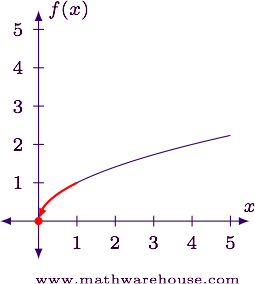
Note that $$x=0$$ is the left-endpoint of the functions domain: $$[0,\infty)$$, and the function is technically not continuous there because the limit doesn't exist (because $$x$$ can't approach from both sides).
We should note that the function is right-hand continuous at $$x=0$$ which is why we don't see any jumps, or holes at the endpoint.
Mixed Discontinuities
Consider the graph shown below.
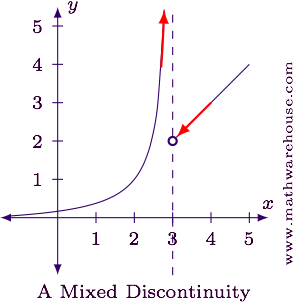
The function is obviously discontinuous at $$x = 3$$. From the left, the function has an infinite discontinuity, but from the right, the discontinuity is removable. Since there is more than one reason why the discontinuity exists, we say this is a mixed discontinuity


















