Quick Overview
- Definition: $$\displaystyle\lim\limits_{x\to a} f(x) = f(a)$$
- A function is continuous over an interval, if it is continuous at each point in that interval.
Motivating Example
Of the five graphs below, which shows a function that is continuous at $$x = a$$?
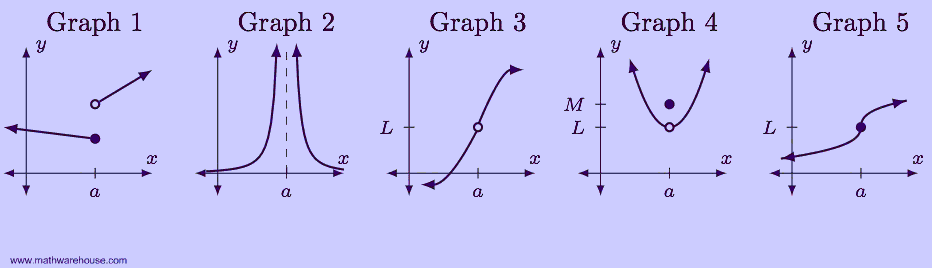
Only the last graph is continuous at $$x = a$$. In each of the first four graphs, there is some aspect that make them discontinuous at $$x=a$$. Understanding what is happening in the first four graphs is important to understanding continuity.
Graphs 1 and 2Notice that for these two graphs, $$\displaystyle\lim\limits_{x\to a} f(x)$$ does not exist, but the limit does exist in all the others, including the continuous one. We might surmise (correctly) that the existence of a limit is important to continuity.
Graph 3In this graph, $$\displaystyle\lim\limits_{x\to a} f(x) = L$$, but the function is undefined. On the hand, Graph 5, the continuous graph is defined at $$x = a$$.
Graph 4If we compare this graph to the fifth one, these two have 2 things in common. In both, the limit exists and the function is defined. However, there is a difference. In graph 4, the value of the limit is different from the value of the function, Specifically, $$\displaystyle\lim\limits_{x\to a} f(x) = L$$, and $$f(a) = M$$.
Graph 5In this graph, $$\displaystyle\lim\limits_{x\to a} f(x) = L$$, and $$f(a) = L$$. That is, the limit exists, the function exists, and they have the same value. It is also the only graph above that is continuous at $$x=a$$.
 Summary
Summary
In the only graph that was continuous at $$x = a$$, we saw that (1) the limit existed, (2) the function was defined, and (3) the limit value was the same as the function value. This is the essence of the definition of continuity at a point.
Definition of Continuity at a Point
A function, $$f(x)$$, is continuous at $$x=a$$ if
$$\displaystyle\lim_{x\to a} f(x) = f(a)$$
Sometimes, this definition is written as 3 criteria:
A function, $$f(x)$$, is continuous at $$x=a$$ as long as
- $$f(a)$$ is defined
- $$\displaystyle\lim\limits_{x\to a} f(x)$$ exists, and
- the two values are equal.
Continuity Over an Open Interval
Consider the function shown in the graph below.
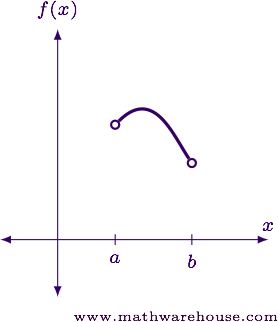
Since the function is continuous at every point in between $$a$$ and $$b$$ we say that $$f(x)$$ is continuous over the open interval $$(a,b)$$.
One-sided Continuity
We can define one-sided continuity using one-sided limits:
Left-Hand Continuity: $$f(x)$$ is left-hand continuous at $$x = a$$ if
$$\displaystyle\lim_{x\to a^-} f(x) = f(a)$$
Right-Hand Continuity: $$f(x)$$ is right-hand continuous at $$x=a$$ if
$$\displaystyle\lim_{x\to a^+} f(x) = f(a)$$
One-sided continuity is important when we want to discuss continuity on a closed interval.
Continuity on a Closed Interval
With one-sided continuity defined, we can now talk about continuity on a closed interval. Specifically:
$$f(x)$$ is continuous on the closed interval $$[a,b]$$ if it is continuous on $$(a,b)$$, and one-sided continuous at each of the endpoints.
Example
Estimate the interval over which the function shown below continuous.
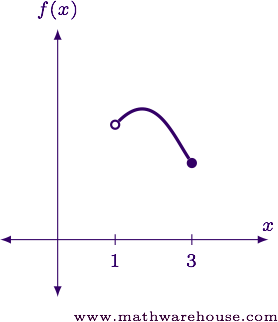
The only "hole" in the graph occurs at $$x=1$$. The function appears to be continuous everywhere else, and left-continuous at $$x= 3$$.
Answer: The function appears to be continuous over $$(1,3)$$.















