- One-sided limits are the same as normal limits, we just restrict $$x$$ so that it approaches from just one side
- $$x\to a^+$$ means $$x$$ is approaching from the right.
- $$x\to a^-$$ means $$x$$ is approaching from the left.
Examples
Example 1
Use the graph to approximate the value of both one-sided limits as $$x$$ approaches 3.
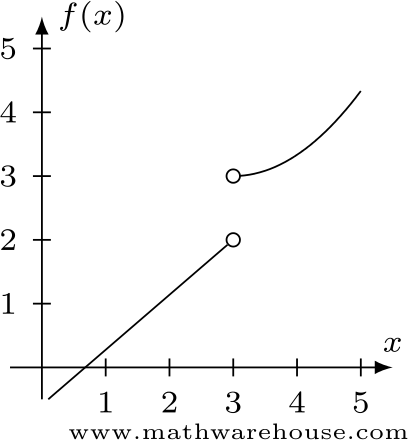
Examine what happens as $$x$$ approaches from the left.
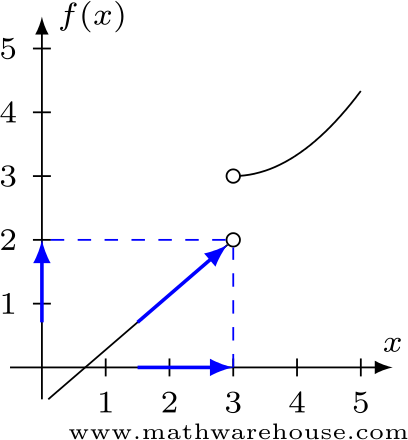
As $$x$$ approaches 3 from the left, the function seems to be approaching 2.
Examine what happens as x approaches from the right
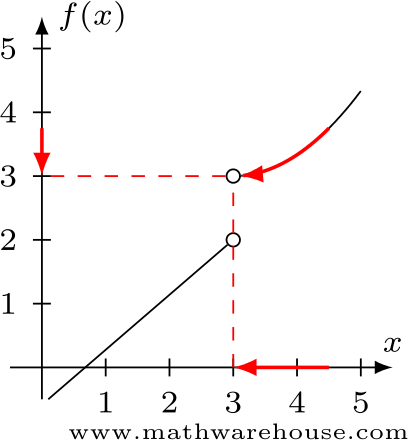
As $$x$$ approaches 3 from the right, the function seems to be approaching 3.
Right-hand limit: $$\displaystyle \lim_{x\to3^+} f(x) \approx 3$$
Example 2: Using Tables
Using the tables below, what can be said about the one-sided limits as $$x$$ approaches 6?
$$ \begin{array}{l|c} x & f(x)\\\hline \hline 5 & 8.32571\\\hline 5.5 & 8.95692\\\hline 5.9 & 8.99084\\\hline 5.99 & 8.99987\\\hline 5.999 & 8.99992\\\hline 5.9999 & 8.99999\\\hline \end{array} $$
$$ \begin{array}{l|c} x & f(x)\\\hline \hline 7 & 1\\\hline 6.5 & 95\\\hline 6.1 & 1230\\\hline 6.01 & 9658\\\hline 6.001 & 54231\\\hline 6.0001 & 834366 \end{array} $$
Examine what happens as $$x$$ approaches 6 from the left.
As $$x$$ approaches 6 from the left...
$$ \begin{array}{l|c} x & f(x)\\\hline \hline 5 & 8.32571\\\hline 5.5 & 8.95692\\\hline 5.9 & 8.99084\\\hline 5.99 & 8.99987\\\hline 5.999 & 8.99992\\\hline 5.9999 & 8.99999 \end{array} $$
...the function seems to be getting closer to 9.
Examine what happens as $$x$$ approaches 6 from the right.
As $$x$$ approaches 6 from the left...
$$ \begin{array}{l|c} x & f(x)\\\hline \hline 7 & 1\\\hline 6.5 & 95\\\hline 6.1 & 1230\\\hline 6.01 & 9658\\\hline 6.001 & 54231\\\hline 6.0001 & 834366 \end{array} $$
...the function seems to just keep getting bigger.
$$\displaystyle\lim\limits_{x\to 6^+} f(x)$$ does not exist.
Practice Problems
Use the graph below to find the limits in questions 1--4.
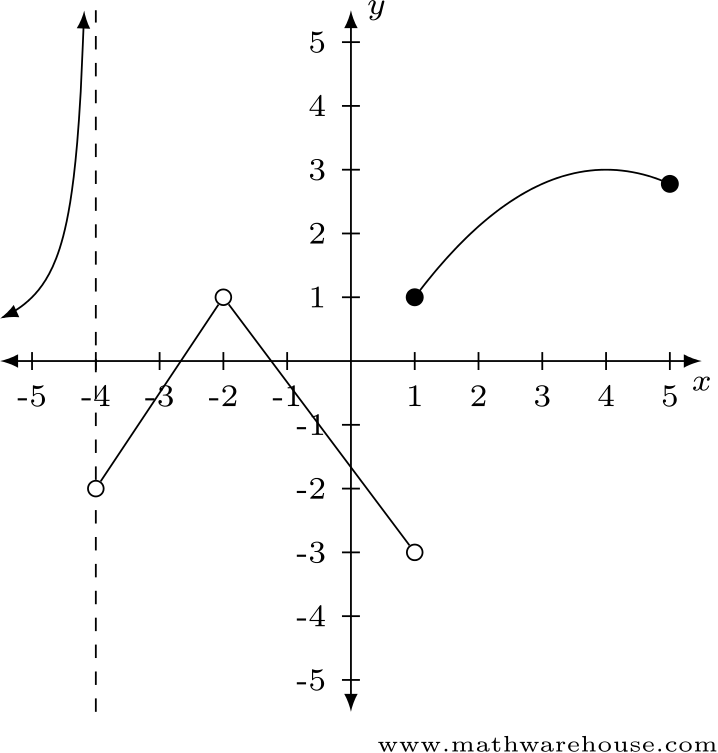
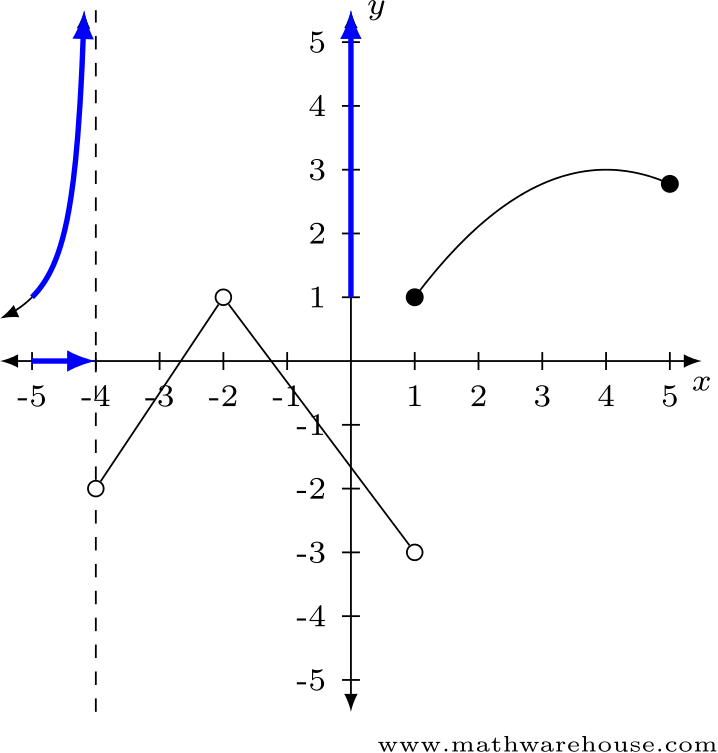Answer: $$\displaystyle\lim\limits_{x\to-4^-} f(x)$$ does not exist.
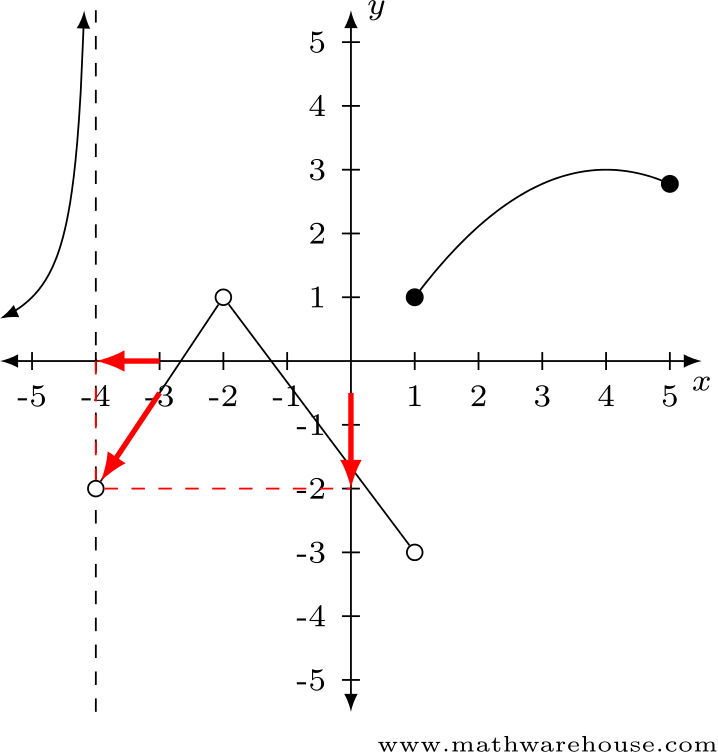Answer: $$\displaystyle\lim\limits_{x\to-4^+} f(x) \approx -2$$
Answer: $$\displaystyle\lim\limits_{x\to 1^-} f(x) \approx -3$$
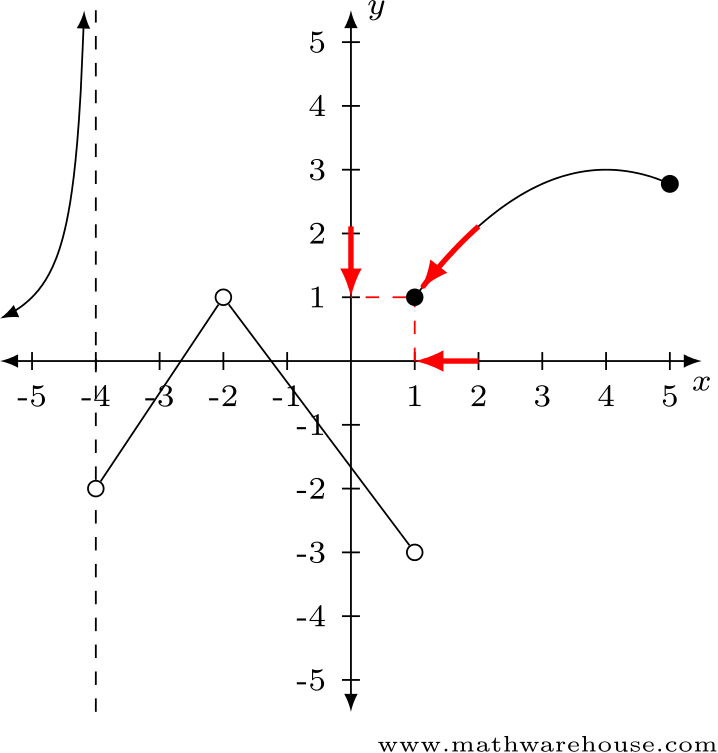Answer: $$\displaystyle\lim\limits_{x\to1^+} f(x) \approx 1$$
Examine what happens as $$x$$ approaches -4 from the left.
As $$x$$ approaches -4 from the left...
$$ \begin{array}{l|c} x & f(x)\\\hline \hline -5 & -4.5\\\hline -4.5 & -44.5\\\hline -4.1 & -444.5\\\hline -4.01 & -4444.5\\\hline -4.001 & -44444.5\\\hline -4.0001 & -444444.5 \end{array} $$
...the function just keeps getting bigger.
Examine what happens as $$x$$ approaches -4 from the right.
As $$x$$ approaches -4 from the right...
$$ \begin{array}{l|c} x & f(x)\\\hline \hline -3 & 2.13671\\\hline -3.5 & 2.52240\\\hline -3.9 & 2.59684\\\hline -3.99 & 2.59987\\\hline -3.999 & 2.59990\\\hline -3.9999 & 2.59999 \end{array} $$
...the function seems to get closer to 2.6.
