Quick Overview
- On graphs, the open and closed circles, or vertical asymptotes drawn as dashed lines help us identify discontinuities.
- As before, graphs and tables allow us to estimate at best.
- When working with formulas, getting zero in the denominator indicates a point of discontinuity.
- When working with piecewise-defined functions, check for discontinuities at the transition points where one piece ends and the next begins.
Examples
Example 1
Using the graph shown below, identify and classify each point of discontinuity.
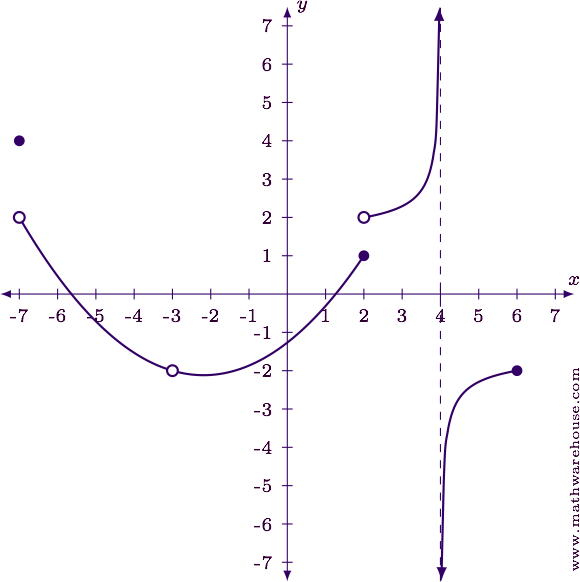 Step 1
Step 1
The table below lists the location ($$x$$-value) of each discontinuity, and the type of discontinuity.
$$ \begin{array}{c|l} {x} & {\mbox{Type}}\\ \hline -7 & \mbox{Mixed}\\ -3 & \mbox{Removable}\\ 2 & \mbox{Jump}\\ 4 & \mbox{Infinite}\\ 6 & \mbox{Endpoint} \end{array} $$
Note that the discontinuity at $$x=-7$$ is both removable (the function value is different from the one-sided limit value) and an endpoint (since the graph is not defined to the left of $$x=-7$$).
Example 2
Using the tables below, what type of discontinuity seems to exist at $$x = 5$$?
$$ \begin{array}{c|lcc|l} {x} & {f(x)}\\ \hline 4.9 & 8.15\\ 4.99 & 8.015\\ 4.999 & 8.0015\\ 4.9999 & 8.00015\\ 4.99999 & 8.000015\\ \end{array} $$
$$ \begin{array}{c|lcc|l} {x} & {f(x)}\\ \hline 5.1 & 2.4\\ 5.01 & 2.43\\ 5.001 & 2.403\\ 5.0001& 2.4003\\ 5.00001 & 2.40003 \end{array} $$
Examine the one-sided limits.
The table on the left tells us $$\lim\limits_{x\to5^-}f(x) \approx 8$$
The table on the right tells us $$\lim\limits_{x\to5^+}f(x) \approx 2.4$$
AnswerThe tables lead us to believe the one-sided limits are different, so we conclude the function likely has a jump discontinuity at $$x = 5$$.
Example 3
Is the function below continuous at its transition point? If not, identify the type of discontinuity occurring there.
$$ f(x) = \left\{% \begin{array}{ll} x^2, & x\leq 1\\ x+3, & x > 1 \end{array} \right. $$
Step 1Identify the transition point(s).
The transition point is at $$x = 1$$ since this is where the function transitions from one formula to the next.
Step 2Determine the left-hand limit at the transition point.
$$ \displaystyle\lim_{x\to 1^-} f(x) = \displaystyle\lim_{x\to 1^-} x^2 = 1^2 = 1 $$
Step 3Determine the right-hand limit at the transition point.
$$ \displaystyle\lim_{x\to 1^+} f(x) = \displaystyle\lim_{x\to 1^+} (x+ 3) = 1 + 3 = 4 $$
AnswerSince the one-sided limits are different, the function has a jump discontinuity at $$x = 1$$.
Example 4
Is the function below continuous at x = 4? If not, identify the type of discontinuity occurring there.
$$ f(x) = \left\{% \begin{array}{ll} \sqrt x, & 0\leq x < 4\\ 5,& x = 4\\ 6 - x, & x > 4 \end{array} \right. $$
Step 1Examine the left-hand limit.
$$ \displaystyle\lim_{x\to 4^-} f(x) = \displaystyle\lim_{x\to 4^-} \sqrt x = \sqrt{4} = 2 $$
Step 2Examine the right-hand limit.
$$ \displaystyle\lim_{x\to 4^+} f(x) = \displaystyle\lim_{x\to 4^+} (6-x) = 6 -4 = 2 $$
Step 3Determine the function value.
$$ f(4) = 5 $$
AnswerThe limit exists, and the function exists, but they have different values. The function has a removable discontinuity at $$x = 4$$.
Example 5
Without graphing, determine the type of discontinuity the function below has at $$x = 3$$.
$$ f(x) = \frac{x^2 + 2x - 15}{x^2-2x-3} $$
Step 1Evaluate $$f(3)$$
$$ f(\blue 3) = \frac{(\blue{3})^2 + 2(\blue{3}) - 15}{(\blue{3})^2-2(\blue{3})-3} = \frac{9 + 6 - 15}{9-6-3} = \frac 0 0 $$
The function is undefined at $$x = 3$$, so there is a discontinuity at this point. To determine the type, we will need to evaluate the limit as $$x$$ approaches 3.
Step 2Since the function has a $$\frac 0 0$$ form at $$x = 3$$, we need to find and divide out the common factors in the numerator and denominator.
$$ \frac{x^2 + 2x - 15}{x^2-2x-3} = \frac{(x+5)\blue{(x-3)}}{\blue{(x-3)}(x+1)} = \frac{x+5}{x+1} $$
Step 3Evaluate the limit of the simpler function as $$x$$ approaches 3.
$$ \displaystyle\lim_{\blue{x\to3}} \frac{x+5}{x+1} = \frac{\blue 3 + 5}{\blue 3 + 1} = \frac 8 4 = 2 $$
AnswerSince the limit exists, but the function value does not, we know the function has is a removable discontinuity at $$x = 3$$.
Example 6
Without graphing, determine the type of discontinuity the function below has at $$x = -1$$.
$$ f(x) = \frac{x^2 + 2x - 15}{x^2-2x-3} $$
Step 1Evaluate $$f(-1)$$
$$ f(\blue{-1}) = \frac{(\blue{-1})^2 + 2(\blue{-1}) - 15}{(\blue{-1})^2-2(\blue{-1})-3} = \frac{1 - 2 - 15}{1+2-3} = \frac{-16} 0 $$
Since we have division by zero, the function doesn't exist at $$x = -1$$. But, the $$\frac n 0$$ form tells us the function is becoming infinitely large as $$x$$ approaches -1.
Note: In order to determine if the limit is infinite, we would need to know which direction the function is going as $$x$$ approached -1. But for the purposes of classifying the discontinuity, it's enough to know the function becomes infinitely large.
AnswerThe function has an infinite discontinuity at $$x = -1$$.


















