If $$f(x)$$ gets really, really, really close to $$\color{purple}L$$ when $$x$$ gets really, really, really y close to $$\color{green}a$$, then we call $$\color{purple}L$$ the limit of the $$f$$
Definition of the Limit of a Function
Suppose $$f(x)$$ becomes arbitrarily close to some particular, finite value $$\color{purple}L$$ as $$x$$ becomes arbitrarily close to some value $$ \color{green}a$$. Then, we say " $$\color{purple}L$$ is the limit of $$f$$ as $$x$$ approaches $$\color{green}a$$" , and we write this as
$$\displaystyle \lim_{x\to \color{green}a} f(x) = \color{purple}L$$
Examples
Example 1: The Limit Exists
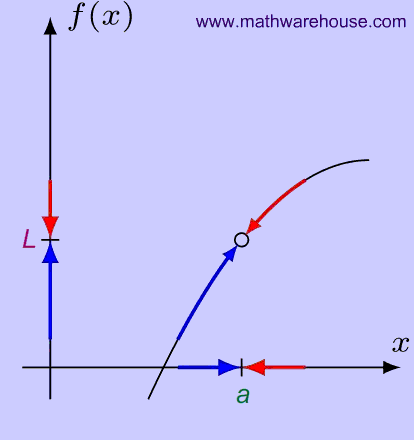
Whether $$x$$ approaches $$a$$ from the left or from the right , the function approaches $$L$$ .
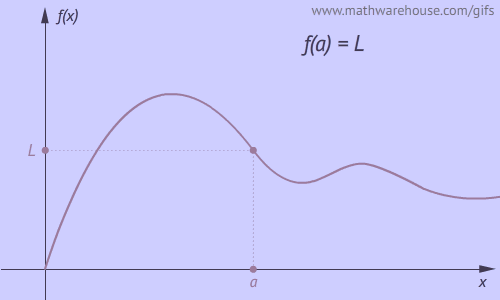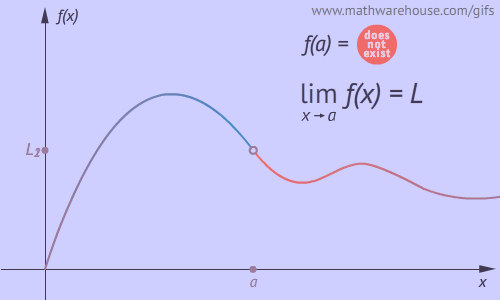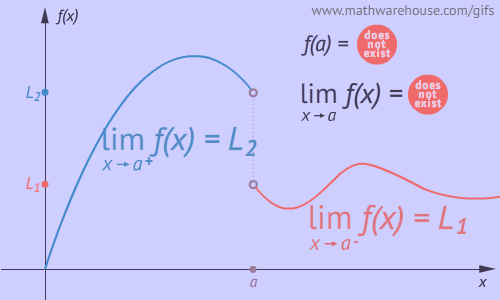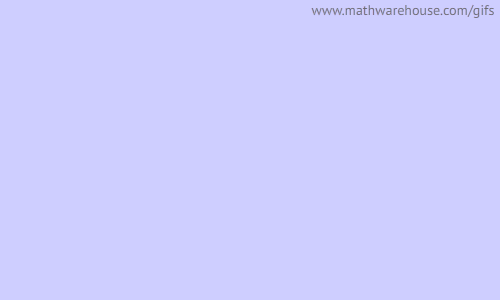
Example 2: Direction Independence Fails
In order for $$a$$ limit to exist, the value the function approaches must be independent of the direction the $$x$$-value comes from. This was the case in Example 1 above. By contrast, the function below approaches two different values as $$x$$ approaches $$a$$ .
$$y$$ approaches two different values...
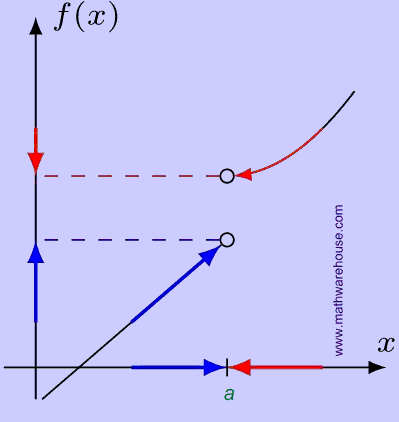
...depending on which direction $$x$$ approaches from.
In this example, the value the function approaches depends on the direction, so 
the function does not have $$a$$ limit as $$x$$ approaches $$a$$.
Example 3: No Finite Value
Another important part of the definition is that the function must approach a finite value. It cannot become infinitely large, as in the example below.
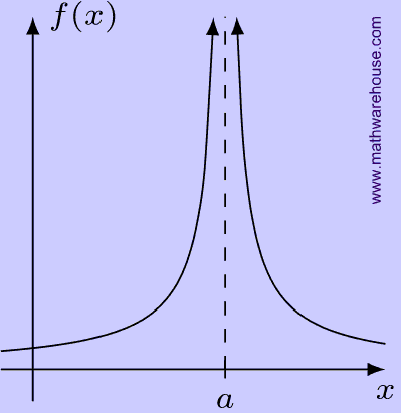
The limit as $$x$$ approaches $$a$$ does not exist because the function values are becoming infinitely large as $$x$$ gets closer to a.
Remember
- This approach must be independent of direction
- The value that $$f(x)$$ approaches must be finite. In our examples, the finite value was always called $$\color{purple}L$$. On the other hand, Example 3 illustrates a situation that does not satisfy this requirement of the basic definition of a limit because in example 3 there is no finite value that $$f(x)$$ approaches.
