Mathwarehouse Logo

Vertical Line Test

What is the Vertical Line Test for Functions?

Answer: A method to distinguish functions from relations.

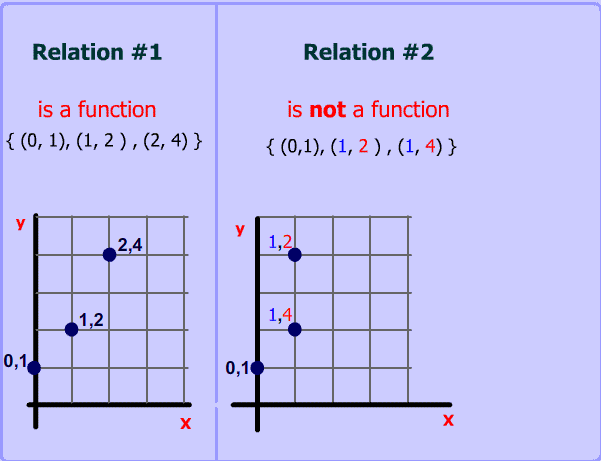
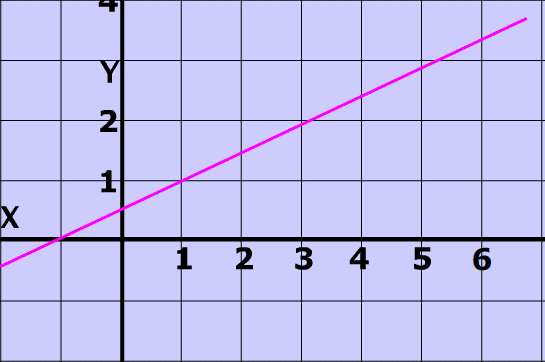
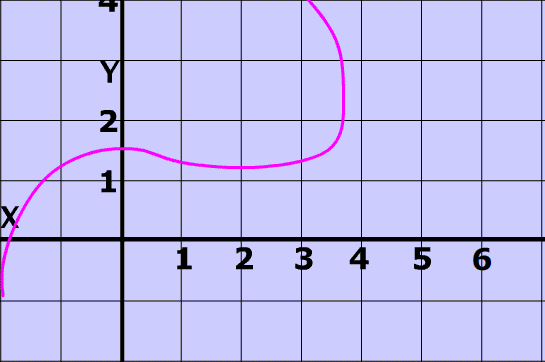
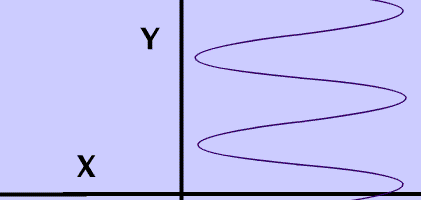
The vertical Line test.

  • is a way to determine if a relation is a function.
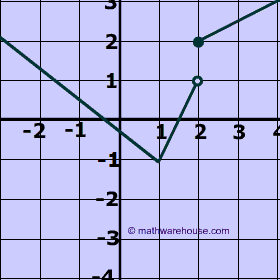
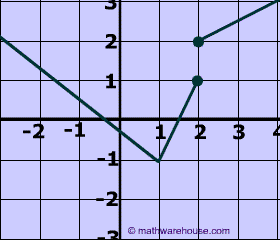
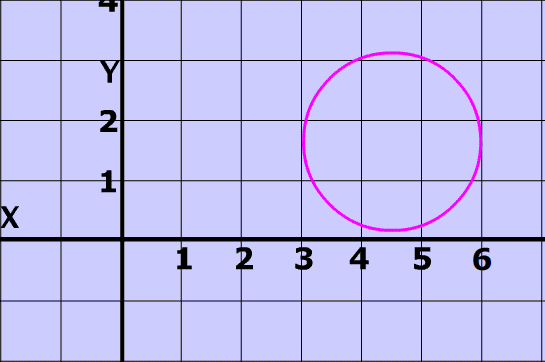
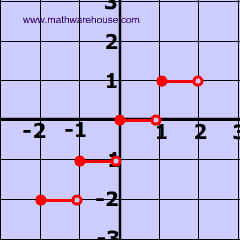
  • states that if a vertical line intersects the graph of the relation more than once, then the relation is a NOT a function.

If you think about it, the vertical line test is simply a restatement of the definition of a function.

Definition of a function: Every x value has a unique y value.

Think about it If any particular x value has 2 different y values, then a vertical line will intersect the at two different places.

Let's examine the two relations below this These two relations differ by only 1 number!

Picture of vertical line test

Practice Problems

Problem 1

Does the graph below represent a function or a relation?

Vertical Line test practice graph

Ask yourself: "Can I draw a vertical line (anywhere) that will hit the graph two time?"

Answer: NO vertical lines only hit the graph once so this is a function.

Problem 2

Does the graph below represent a function or a relation?

Vertical Line test practice graph

Ask yourself: "Can I draw a vertical line (anywhere) that will hit the graph two times?"

Answer: YES a vertical line can hit the graph twice so this is not a function.

Problem 3

Does the graph below represent a function or a relation?

Vertical Line test practice graph

Ask yourself: "Can I draw a vertical line (anywhere) that will hit the graph two times?"

Answer: YES a vertical line hits the graph several times, so this is not is a function.

Problem 4

Does the graph below represent a function or a relation?

Vertical Line test practice graph

Ask yourself: "Can I draw a vertical line (anywhere) that will hit the graph two times?"

Answer: NO matter where you try to draw a vertical line, it only hits the graph once so this is a function.

Be careful at x =2. The point (2, 1) is not filled in, indicating that the graph does not include the point (2, 1). However, notice that (2, 2) is completely filled in, because that point is included in the graph.

Problem 5

Does the graph below represent a function or a relation? (look carefully, this graph is slightly different from the prior problem's graph).

Vertical Line test practice graph

Ask yourself: "Can I draw a vertical line (anywhere) that will hit the graph two times?"

Answer: Yes, a vertical line can intersect this function more than once! .

Unlike problem 3, in this case, the point (2, 1) is filled in and is,therefore, included in the graph.

As you can see, that one point makes all the difference.

This is not a function

Problem 6

Does the graph below represent a function or a relation? (look carefully, this graph is slightly different from the prior problem's graph).

Vertical Line test practice graph

Ask yourself: "Can I draw a vertical line (anywhere) that will hit the graph two times?"

Answer: YES This is not a function . In fact, circles, in general, are not functions.

Problem 7

Does the graph below represent a function or a relation? (look carefully, this graph is slightly different from the prior problem's graph).

Vertical Line test practice graph

Ask yourself: "Can I draw a vertical line (anywhere) that will hit the graph two times?"

Answer: NO This is a function
Back to Functions Next to Composition of Functions

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!