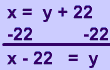What is the Inverse of a function?
A conceptual analogyIf the function itself is considered a "DO" action, then the inverse is the "UNDO".
What about the domain and Range?
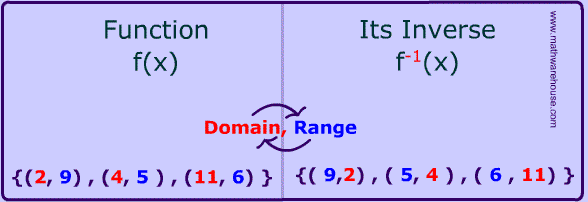
Definition: The inverse of a function is when the domain and the range trade places. All elements of the domain become the range, and all elements of the range become the domain.
Therefore, the inverse of a function is equivalent to what kind of transformation?
Reflection over the line y = x.
Another Example
| Original function f(x) | Inverse of function or f-1(x) |
|---|---|
{(0, 3) , (1, 4) , (2, 5)} |
{(3, 0) , (4, 1) , (5, 2)} |
Is the inverse of a function always a function?
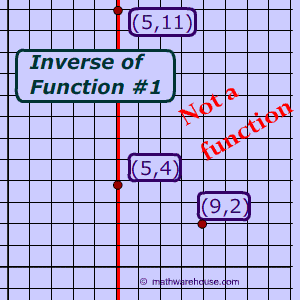
To answer that question let's look at the function in Diagram 1. In that graph, you can see
the original function and its inverse .
Is the inverse of that function , also a function?
No
As you can see, the inverse of that function does not pass the vertical line test and, therefore , is not a function.
Diagram I
![Picture of inverse of a function]( "Inverse of A Function Picture")
Conclusion: The inverse of a function is not necessarily a function.
So...when is the inverse of a function also a function?
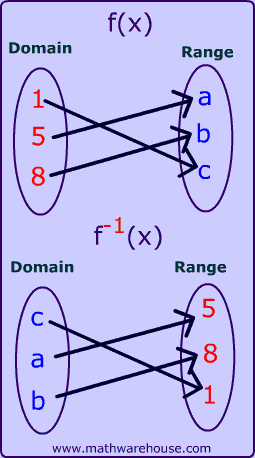
f-1(x), the inverse, is itself a function only when f(x), the original function, is a one-to-one function.
Remember: 1 to 1 functions must pass the horizontal line test!
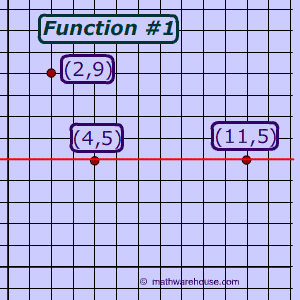
Example 1In this case, f(x) is a function, but f-1(x) is nota function.
Function #1, f(x) is not a one to one function because it does not pass the horizontal line test .
. f-1(x) is not a function.
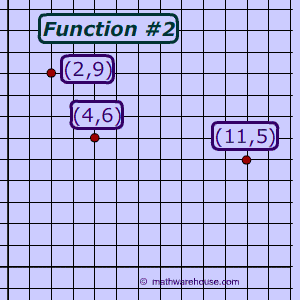
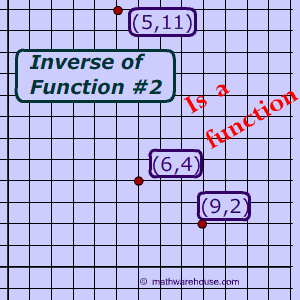
In this case, f(x) is a function and f-1(x) is also a function.
This function passes the horizontal line test so, its inverse will also be a function.
Practice Problems Part I
Problem 1
Remember: $$ f^{-1} (x) $$ means 'the inverse of f(x) '.
$$ f^{-1} (x) $$ = {(2, 1) , (4, 3) , (6, 5)}
Problem 2
Remember: $$ f^{-1} (x) $$ means 'the inverse of f(x) '.
$$ f^{-1} (x) $$ = {(14, 33) , (15, 23) , (12, 11) , (14, 13)}}
Problem 3
Remember: $$ f^{-1} (x) $$ means 'the inverse of f(x) '.
$$ f^{-1} (x) $$ = {(12, -1) , (114, 13) , (61, 15) , (12, 1)}
Problem 4
y = 3 is a horizontal line. In a horizontal line all elements of the range are 3.
So, it looks something $$ f^{-1} (x) $$ ={(-1,3) , (0, 3) , (1, 3)}.
Therefore the inverse of this function will be whatever line has 3 for all elements in its domain.
Therefore the inverse of y = 3 is the line x = 3.
Solving Algebraically for the Inverse
What is the inverse of f(x) = x + 1?
Just like in our prior examples, we need to switch the domain and range. I n an equation, the domain is represented by the x variable and the range by the y variable.
To Summarize
f(x): took an element from the domain and added 1 to arrive at the corresponding element in the range.
f-1(x) : took an element from the domain and subtracted 1 to arrive at the corresponding element in the range.
Practice Problems Part II
Problem 1
Step 1
Replace f(x) with y.
$$ y = x + 22 $$
Step 2
![switch x and y]()
Switch x and y.
$$ x = y + 22 $$
Step 3
![work]()
Solve for new 'y'.
Step 4
Replace 'y' with f-1(x).
$$ f^{-1} (x) = x - 22 $$
Problem 2
Step 1
Replace f(x) with y.
$$ y = 2x $$
Step 2
![switch x and y]()
Switch x and y.
$$ x = 2y $$
Step 3
Solve for new 'y'.
$$ \frac{1}{2} x = \frac{1}{2} \cdot 2y \\ \frac{1}{2} x = y $$
Step 4
Replace 'y' with f-1(x).
$$ f^{-1} (x) =\frac{1}{2} x $$
Problem 3
Step 1
Replace f(x) with y.
$$ y = \frac{1}{2}x + 3 $$
Step 2
![switch x and y]()
Switch x and y.
$$ x = \frac{1}{2}y + 3 $$
Step 3
Solve for new 'y'.
$$ \color{Red}{2 \cdot} x = \color{Red}{2 \cdot} \big (\frac{1}{2}y + 3 \big) \\ 2 \cdot x = \frac{2}{2}\cdot y + 2 \cdot 3 \\ 2x = y + 6 \\ 2x -6 = y $$
Step 4
Replace 'y' with f-1(x).
$$ f^{-1} (x) = 2x -6 $$
Problem 4
Step 1
Replace f(x) with y.
$$ y = x^2 + 3 $$
Step 2
![switch x and y]()
Switch x and y.
$$ x = y^2 + 3 $$
Step 3
Solve for new 'y'.
$$ x \color{Red}{-3} = y^2 + 3 \color{Red}{-3} \\ x -3 = y^2 \\ \sqrt{x-3} = \sqrt{y^2} \\ \sqrt{x-3} = y $$
Step 4
Replace 'y' with f-1(x).
$$ f^{-1} (x) = \sqrt{x-3} $$
Problem 5
Step 1
Replace f(x) with y.
$$ y = 5 \sqrt{x} $$
Step 2
![switch x and y]()
Switch x and y.
$$ x = 5 \sqrt{y} $$
Step 3
Solve for new 'y'.
$$ x{\color{Red}{^2}} = \big(5 \sqrt{y} \big) {\color{Red}{^2}} \\ x^2 = 5{\color{Red}{^2}} \cdot (\sqrt{y}){\color{Red}{^2}} \\ x^2 = 25y \\ \frac{1}{25} \cdot x^2 = \frac{1}{25} \cdot 25y \\ \frac{1}{25} \cdot x^2 = y $$
Step 4
Replace 'y' with f-1(x).
$$ f^{-1} (x) = \frac{1}{25} \cdot x^2 $$
