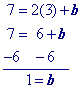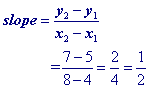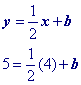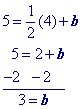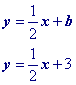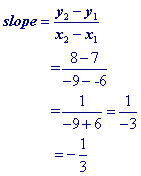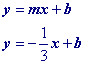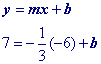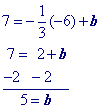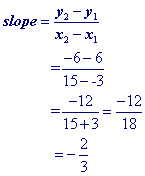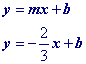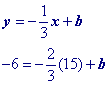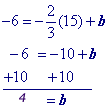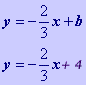Find Equation of Line From 2 Points. Example, Practice Problems and Video Tutorial

What Type of Equation?

Point Slope or Slope Intercept ?

There are a few different ways to write the equation of line .

Slope Intercept Form

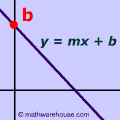
The first half of this page will focus on writing the equation in slope intercept form like example 1 below.

Point Slope Form

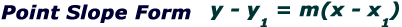
However, if you are comfortable using the point slope form of a line, then skip to the second part of this page because writing the equation from 2 points is easier with point slope form.

Which Form is better?

Point Slope Form is better

Point slope form requires fewer steps and fewer calculations overall. This page will explore both approaches. You can click here to see a side by side comparison of the 2 forms.

Video Tutorial
on Finding the Equation of a line From 2 points

Example - Slope Intercept Form

Using Slope Intercept Form

Find the equation of a line through the points (3, 7) and (5, 11)

Step 1

Calculate the slope from 2 points.

$$ \text { slope } \\ \frac{ y_2 - y_1}{x_2 - x_1} \\ \frac{ 11- 7 }{5-3} \\ \frac 4 2 = \boxed{2} $$

Step 2

Substitute the slope for 'm' in the slope intercept form of the equation.

$$ y = \red{m} x + b \\ y = \red 2 x + b $$

Step 3

Substitute either point into the equation. You can use either $$(3, 7)$$ or $$(5, 11)$$.

Let's use $$( \red 3, \red 7)$$

$$ y = 2x + b \\ \red 7 = 2 (\red 3) + b $$

Step 4

Solve for b, which is the y-intercept of the line.

Step 5

Substitute $$ 1$$ for $$ \red b $$ , into the equation from step 2.

$$ y = 2x + \red b \\ y = 2x + \red 1 \\ \boxed { y = 2x + 1 } $$

Use our Calculator

You can use the calculator below to find the equation of a line from any two points. Just type numbers into the boxes below and the calculator (which has its own page here) will automatically calculate the equation of line in point slope and slope intercept forms.

(x₁,y₁)

(x₂,y₂)

Clear

Calculate

Toggle Points

Auto Calculate

Answer:

$ $

Clear

Calculate

Toggle Points

Practice Problems- Slope Intercept Form

Problem 1

Find the equation of a line through the following 2 points: (4, 5) and (8, 7)

Step 1

Calculate the slope from 2 points.

Step 2

Substitute the slope for 'm' in the slope intercept form of the equation.

y = mx +b
y = ½x +b

Step 3

Substitute either point into the equation. You can use either (4, 5) or (8, 7).

Step 3

Step 4

Solve for b, which is the y-intercept of the line.

Step 5

Substitute b, 3, into the equation from step 2.

Problem 2

Find the equation of a line through the following the points: (-6, 7) and (-9, 8).

Step 1

Calculate the slope.

Step 2

Substitute the slope for 'm' in the slope intercept equation.

Step 3

Substitute either point into the equation. You can use either (-6, 7) or (-9, 8).

Step 3

Step 4

Solve for b, which is the y-intercept of the line.

Step 5

Substitute b, 5, into the equation from step 2.

$$ y = \frac{1}{3}x +\red{b} \\ y = \frac{1}{3}x +\red{5} $$

Problem 3

Find the equation of a line through the following the 2 points: (-3, 6) and (15, -6).

Step 1

Calculate the slope.

Step 2

Substitute the slope for 'm' in the slope intercept equation.

Step 3

Substitute either point into the equation. You can use either (-3, 6) or (15, -6).

Step 3

Step 4

Solve for b, which is the y-intercept of the line.

Step 5

Substitute b, -1, into the equation from step 2.

Example 2

Equation from 2 points using Point Slope Form

As explained at the top, point slope form is the easier way to go. Instead of 5 steps, you can find the line's equation in 3 steps, 2 of which are very easy and require nothing more than substitution! In fact, the only calculation, that you're going to make is for the slope.

The main advantage, in this case, is that you do not have to solve for 'b' like you do with slope intercept from.

Find the equation of a line through the points $$(3, 7)$$ and $$(5, 11)$$ .

Step 1

Calculate the slope from the 2 points.

$$ \text { slope } \\ \frac{ y_2 - y_1}{x_2 - x_1} \\ \frac{ 11- 7 }{5-3} \\ \frac 4 2 = \boxed{2} $$

Step 2

Substitute the slope for 'm' in the point slope equation.

$$ y - y_1 = m(x - x_1) \\ y - y_1 = \red 2 (x - x_1) $$

Step 3

Substitute either point as $$ x1, y1 $$ in the equation. You can use either $$(3, 7)$$ or $$ (5, 11) $$.

Using $$ (3, 7)$$ :

$$ y - 7 = 2(x - 3) $$

Using $$ (5, 11)$$ :

$$ y - 11 = 2(x - 5) $$

Practice Problems - Point Slope

Point Slope is definitely the easier form for what we are doing. It takes 2 steps and 1 of the steps is simply substitution! So, really the only thing you have to do is find the slope and then substitute a point.

Problem 1

Find the equation of a line through the following 2 points: (4, 5) and (8, 7).

Step 1

Calculate the slope from 2 points.

Step 2

Substitute the slope for 'm' in the point slope equation.

y - y₁ = m(x - x₁)
y - y₁ = ½(x - x₁)

Step 3

Substitute either point into the equation. You can use either (4, 5) or (8, 7).

using (4, 5):
y - 5 = ½(x - 4)

using (5, 11) :
y - 11 = ½(x - 5)

Problem 2

If a line goes through the following 2 points, what is the line's equation? (-6, 7) and (-9, 8).

Step 1

Calculate the slope from 2 points.

Step 2

Substitute the slope for 'm' in the point slope equation.

y - y₁ = m(x - x₁)
y - y₁ = ⅓(x - x₁)

Step 3

Substitute either point into the equation. You can use either (-6, 7) or (-9, 8).

using (-6, 7):
y - 7 = ⅓(x + 6)

using (-9, 8):
y - 8 = ⅓(x + 9)

Problem 3

Find the equation of a line through the following the 2 points: (-3, 6) and (15, -6).

Step 1

Calculate the slope from 2 points.

Step 2

Substitute the slope for 'm' in the point slope equation.

y - y₁ = m(x - x₁)
y - y₁ = ⅓(x - x₁)

Step 3

Substitute either point into the equation (-3, 6) and (15, -6).

using (-3, 6):
y - 6 = ⅓(x + 3)

using (15, -6):
y + 6 = ⅓(x - 15)

If you read this whole page and looked at both methods (slope intercept form and point slope), you can see that it's substantially quicker to find the equation of line through 2 points by means of point slope.

Find the equation of a line through the points (3, 7) and (5, 11)