Equation of a line Given slope and A point. Video tutorial and practice problems . It's easy to ...

Video Tutorial on Equation from Slope and a Point

Example Problem

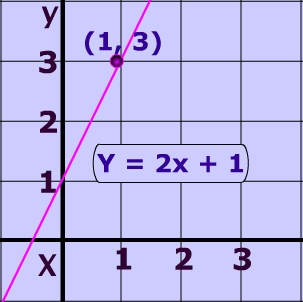
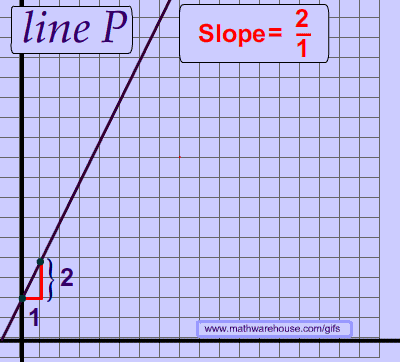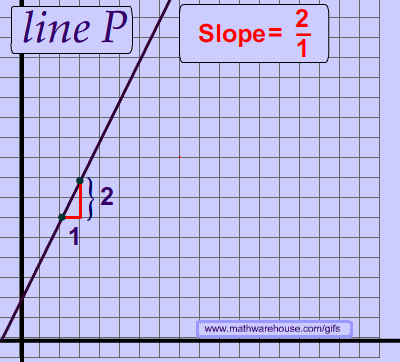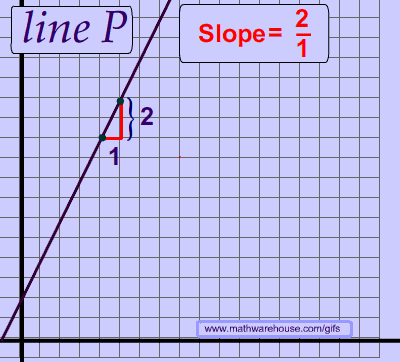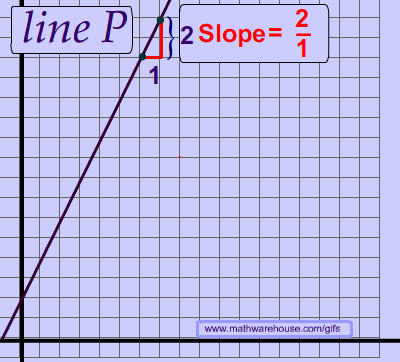
Find the equation of a line that goes through the point (1, 3) and has a slope of 2.

Step 1

Substitute slope for 'm' in y = mx + b.

$$ y = \red m x + b \\ y = \red 2 x + b $$

Step 2

Substitute the point $$ (\red 1, \red 3)$$ into equation.

$$ y = 2x + b \\ \red 3 = 2( \red 1) + b $$

Step 3

Solve for b.

$$ 3 = 2 + \red b \\ 3 - 2 = 1 = \red b $$

Step 4

Now that we know b, all that we have to do is substitute it into the equation, and we now have our line in slope intercept form.

$$ y = 2x + 1 $$

Diagram of Line

Equation of line from its slope and one point

Practice Problems

Directions: For all questions below, express your answers using slope intercept form.

Problem 1

Write the equation of a line that has a slope of $$ \frac 1 2 $$ and that goes through the point $$ (2, 3)$$.

Step 1

Substitute slope for 'm' in the slope intercept form.

$$ y = \red{ m } x + b \\ y = \red{ \frac 1 2 } x + b $$

Step 2

Substitute x and y coordinates of given point, $$ (2, 3) $$ .

$$ \red 3 = \frac 1 2 (\red 2)+ b $$

Step 3

Solve equation for b.

$$ 3 = 1 + \red b \\ 3 - 1 = \red b \\ 2 = \red b $$

Last Step

Substitute b into equation.

$$ y = \frac 1 2 x + 2 $$

Below is graph of $$ y = \frac 1 2 x + 2 $$ .

Problem 2

The slope of a line is $$ 10$$ and the line goes through the point $$ (3, 34) $$. Express the equation of this line in slope-intercept form.

Step 1

Substitute given slope for $$\red m $$ in the slope intercept form.

$$ y = \red m x + b \\ y = \red {10} x + b $$

Step 2

Substitute x and y coordinates of given point.

$$ y = \red {10} x + b \\ \red { 34 } = 10 (\red 3) + b \\ $$

Step 3

Solve equation for B.

$$ 34 - 30 = b \\ 4 = b $$

Step 4

Substitute b into equation.

$$ y = 10x + 4 $$

Problem 3

The slope of a line is $$ 3$$ and the line goes through the point $$ (6,23)$$ Express the equation of this line in slope-intercept form.

Step 1

Substitute given slope for $$\red m $$ in the slope intercept form.

$$ y = \red m x + b \\ y = \red 3 x + b $$

Step 2

Substitute x and y coordinates of given point.

$$ y = \red 3 x + b \\ 23 = \red 3 (6) + b $$

Step 3

Solve equation for B.

$$ 23 = \red 3 (6) + b \\ 23 = 18 + \red b \\ 5 = b $$

Step 4

Substitute B into equation.

$$ y = 3x + 5 $$

Problem 4

What is the equation of a line whose slope is $$ 0$$ and that goes through the point $$ (7, 5)$$ ? Express the equation of this line in slope-intercept form.

There are two ways to approach this problem.

You can use the steps we have been working on throughout this page (see immediately below).

Or, you can look at this as a horizontal line, any horizontal line has an equation of $$ y = b $$ where b is the y intercept. Since the slope is 0, and only horizontal lines have a slope of zero, all points on this line including the y-intercept must have the same y value. This y-value is $$ \red 5$$, which we can get from the fact that the line passes through the point $$ (7, \red 5) $$. Therefore the equation of this horizontal line is $$ y = 5$$.

Step 1

Substitute given slope for $$\red m $$ in the slope intercept form.

$$ y = \red 0x + b$$

Step 2

Substitute x and y coordinates of given point.

$$ y = \red0 x + b \\ 5 = 0(7) + b $$

Step 3

Solve equation for B.

$$ b = 5$$

Step 4

Plug in B as the y-intercept and write standard form equation.

$$ y = 0x + 5 \\ y = 5 $$