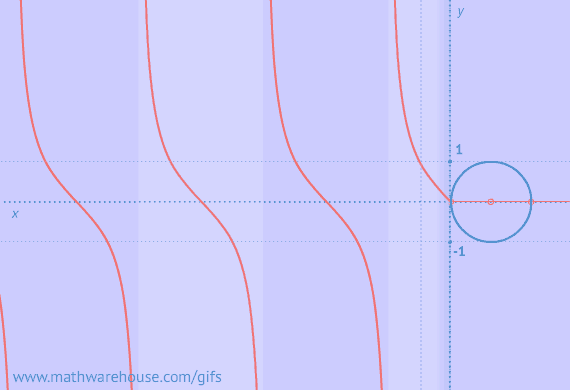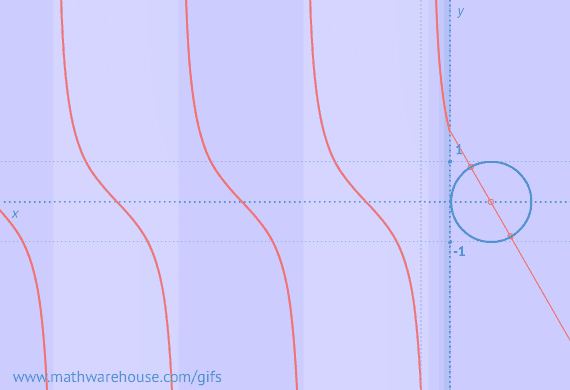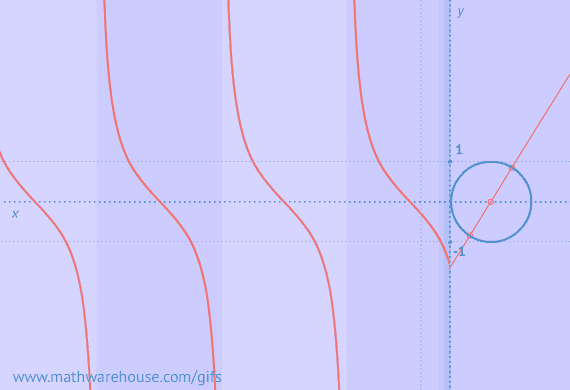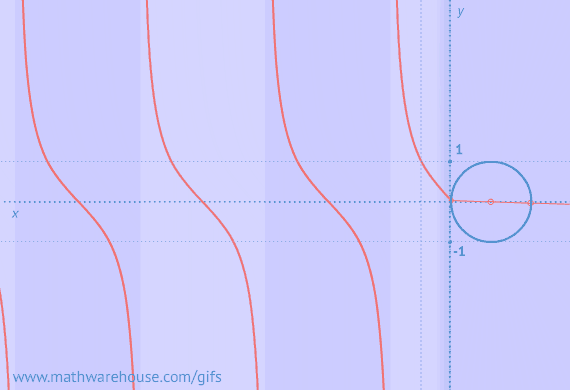
Video Tutorial on the Ambiguous Case
First, something very important to review
Well, the ambiguous case goes back to something you learned in your prior trig lessons and it has to do with a characteristic of the sine function. So, first let's look at something that is always true about the sine function.
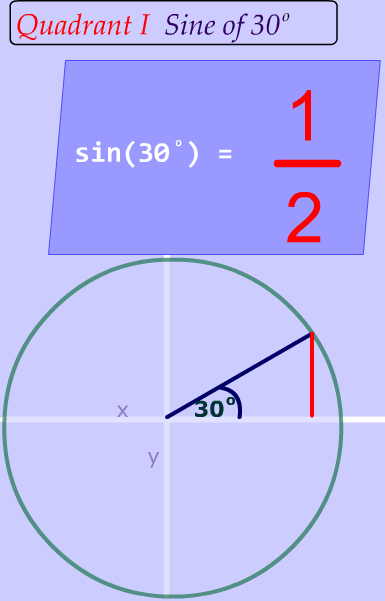
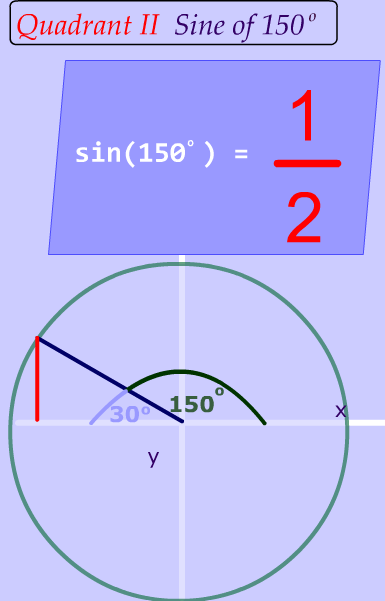
This is a big deal
This is a big deal! And it is the foundation for the ambiguous case of the law of sines. (Remember ambiguous means that something has more than 1 meaning).
As you can see, two different angles have the same sine value !
So, if I asked you :
What angle measurement has a sine value of $$\frac {1}{2} ? $$
You could say two different things--either $$ 30^{\circ}$$ or $$ 150^{\circ} $$ . This is what we mean by ambiguous.
Maybe, you are already getting the idea here. If not, no problem. This is much easier to understand by looking at a specific example .
A Specific Example
The best way to see this ambiguity is to solve a problem using the Law of Sines like normal... and, at the end..you'll notice something.
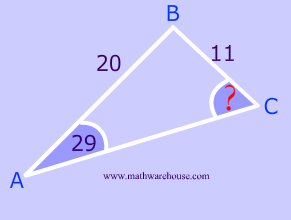
$$
\frac{sin(\blue c)}{20} = \frac{sin(29)}{11}
\\
sin( \blue c ) = \frac{20 \cdot sin(29)}{11}
\\
sin( \blue c ) = \red{ 0.881472 }
\\
m\angle \blue c = sin^{-1}( \red{ 0.881472 } )
\\
$$
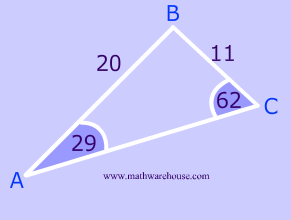
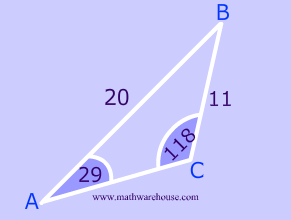
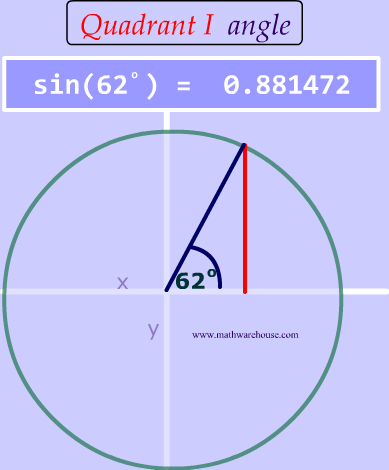
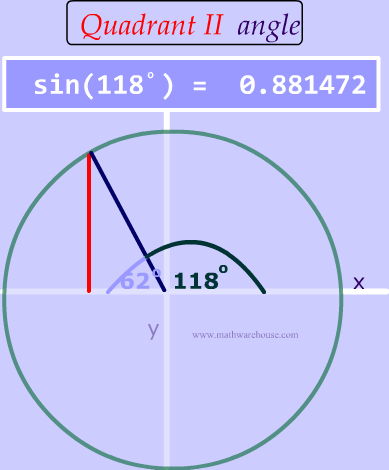
Can we always get 2 triangles?
Answer:In a word ,no
No, sometimes only one triangle is possible. In some cases, zero triangles are possible!
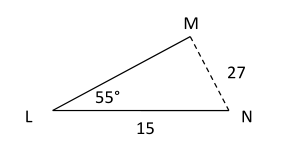
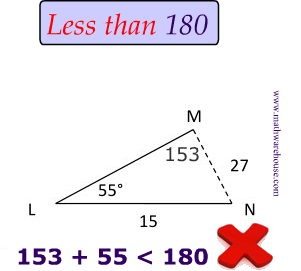
$$ \frac{ sin( \red M)}{15} = \frac{sin(55)}{27} \\ sin( \red M)= \frac{15 \cdot sin(55)}{27} \\ \angle \red M = 27 ^{\circ} \\ $$
$$ \text{What about Quadrant II? } \\ \text{In Quadrant II, we have 153 } \\ \angle \red M = 180-27 = 153 ^{\circ} $$
$ \text{ You can }\red{not} \text{ use } 153^{\circ} \\ $
Because $$\angle L$$ is $$ 55^{\circ} $$ and the total degrees of the angles inside a triangle have to be $$ 180 ^{\circ}$$ .
Take away: The Quadrant II angle will sometimes be too large and in cases like this, there is only 1 solution and only 1 possible triangle.
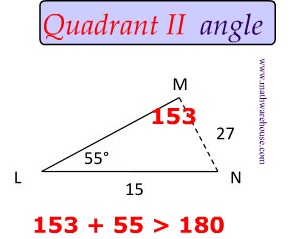
The Rule
The Rule When you add up the given angle ($$55 ^{\circ}$$) and the Quadrant II angle ( $$153^{\circ}$$), the sum must be less than $$180^{\circ} $$ .
This is because you still have a third angle $$\angle N$$ in Triangle 3 below.
A common type of question is to ask how many triangles are possible. As you can see, sometimes there are 2 triangles, sometimes (like the last examples), only one traingle is posssible.
If you're curious about whether or not no triangles are possible, then check this out , but first I recomend you make sure you can do the practice problems below
Steps for Solving Problems
Question: For Triangle 4 below, how many triangles can be formed?
Taken from our free downloadable worksheet
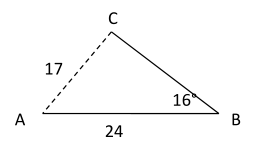
The only angle we can solve for is $$\angle \red c$$
$$ \frac{sin( \red c)}{24} = \frac{sin(16)}{17} \\ sin( \red c)= \frac{24 \cdot sin(16)}{17} \\ \red c= sin^{-1} (\frac{24 \cdot sin(16)}{17}) \\ m\angle \red c \approx 22^{\circ} $$
Note: we found the Quadrant I angle.
Calculate the Quadrant II angle.
$$ \boxed{\text{ Quadrant II}} \\ \red c = 180 - 22^{\circ} \\ m\angle \red c = 158^{\circ} $$
Check to see if the Quadrant II angle is a possible angle measurement for the triangle, using the sum of the angles of a triangle .
$$ 158^{\circ} + 16^{\circ} < 180^{\circ} $$
Answer: In this case, there are 2 different triangles possible .
Practice Problems
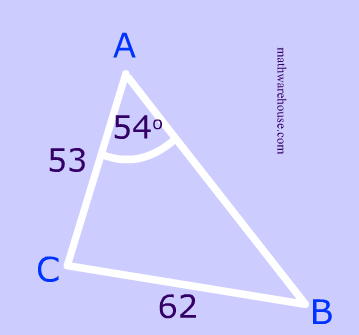
Problem 1
For $$\triangle ABC$$, find all possible values of $$m\angle B $$ to the nearest tenth of a degree.
$$ \frac{sin(\red B)}{53}= \frac{sin(54^{\circ})}{62} \\ sin(\red B)= \frac{53 \cdot sin(54^{\circ})}{62} \\ \red B= sin^{-1} \left( \frac{53 \cdot sin(54^{\circ})}{62} \right) \\ \red B= 43.7 ^{\circ} $$
Calculate the Quadrant II angle.
$$ \boxed{\text{ Quadrant II}} \\ \red B = 180 - 43.7^{\circ} \\ m\angle \red B = 136.3^{\circ} $$
Check to see if the Quadrant II angle is a possible angle measurement for the triangle, using the sum of the angles of a triangle.
$$ 136.3^{\circ} + 54^{\circ} < 180^{\circ} $$
Answer: In this case, there is only 1 possible $$m\angle B$$ , because there is only 1 possible triangle.
To keep practicing similar problems, just scroll to the next one. If you're curious about whether or not, it's possible for there to be zero triangles, then read our article here.
Problem 2
$$ \frac{sin(\red D)}{d}= \frac{sin( E) }{e} \\ \frac{sin(\red D)}{6}= \frac{sin(38^{\circ})}{24} \\ sin(\red D)= \frac{6 \cdot sin(38^{\circ})}{24} \\ \red D = sin^{-1} \left( \frac{6 \cdot sin(38^{\circ})}{24} \right) \\ \red D = 8.9 ^{\circ} $$
Calculate the Quadrant II angle.
$$ \boxed{\text{ Quadrant II}} \\ \red D = 180 - 8.9^{\circ} \\ m\angle \red D = 171.1^{\circ} $$
Check to see if the Quadrant II angle is a possible angle measurement for the triangle, using the sum of the angles of a triangle
$$ 171.1^{\circ} + 38^{\circ} < 180^{\circ} $$
Answer: In this case, there is only 1 possible
Problem 3
$$ \frac{sin(\red L)}{l}= \frac{sin( M) }{m} \\ \frac{sin(\red L)}{30}= \frac{sin(40^{\circ})}{24} \\ sin(\red L)= \frac{30 \cdot sin(40^{\circ})}{24} \\ \red L = sin^{-1} \left( \frac{30 \cdot sin(40^{\circ})}{24} \right) \\ \red L = 53.5 ^{\circ} $$
Calculate the Quadrant II angle.
$$ \boxed{\text{ Quadrant II}} \\ \red L = 180 - 53.5^{\circ} \\ m\angle \red L = 126.5^{\circ} $$
Check to see if the Quadrant II angle is a possible angle measurement for the triangle, using the sum of the angles of a triangle
$$ 126.5^{\circ} + 40^{\circ} < 180^{\circ} $$
Answer: In this case, there are 2 possible $$m\angle L$$ : $$53.5^{\circ} \text{ and } 126.5^{\circ} $$ .
