|
|
|
|
|
|
 
|
Axis of Symmetry of a ParabolaThis page: identify axis of symmetry from a graph | axis of symmetry formula Related Pages: Parabola--graph, equation and formula |Axis of Symmetry |Standard and Vertex Forms of Equation| real world applications | Converting between Standard and Vertex Forms | Tangent of Parabola| area of parabola Axis of Symmetry
Every parabola has an axis of symmetry which is the line that runs down its center. This line divides the graph into two perfect halves.
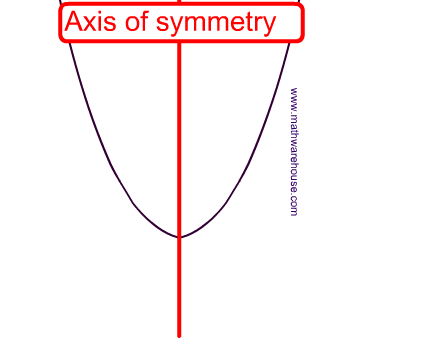
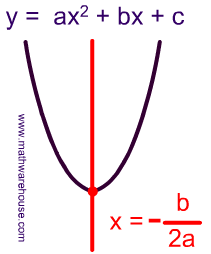
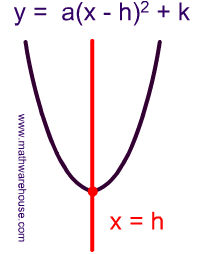
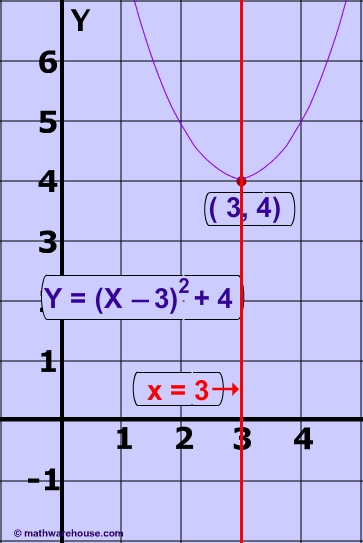
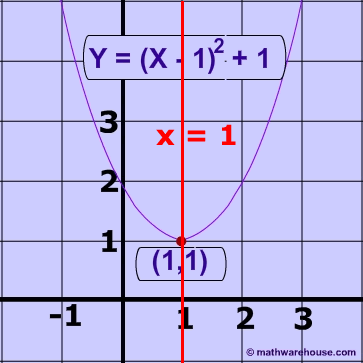
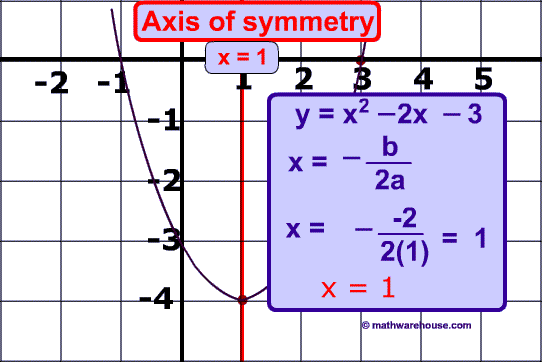
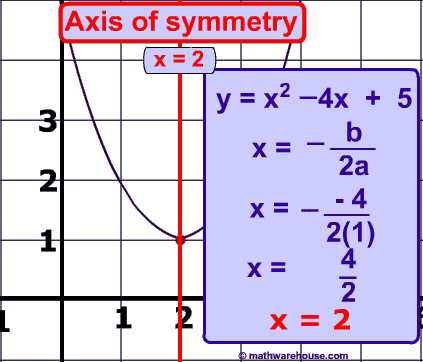
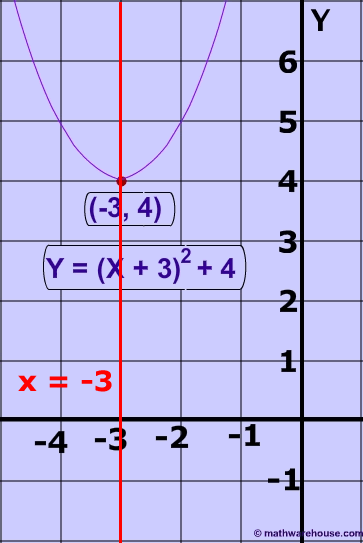
In the picture of on the left, the axis of symmetry is the line x =1. Identify Axis of Symmetry From Graph Problem 1) In the picture on the left, identify the axis of symmetry.
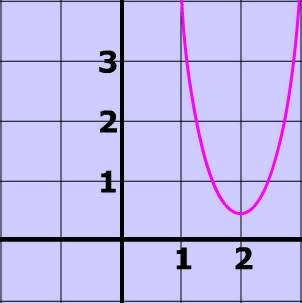
answer It is the line x=2 
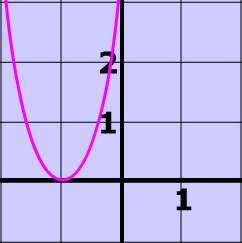
Problem 2) What is the axis of symmetry of the parabola on the left? answer It is the line x = -1 Axis of Symmetry FormulaThere are two different formulas that you can use to find the axis of symmetry. One formula works when the parabola's equation is in vertex form and the other works when the parabola's equation is in standard form.
Practice finding axis of symmetry from Vertex Form Equation
1) What is the following parabola's axis of symmetry
of
y = (x + 3)² + 4
2) What is the axis of symmetry of the parabola y = (x – 3)² + 4
3) What is the axis of symmetry of y = (x–1)² + 1
Practice finding axis of symmetry from Vertex Form Equation Related Pages: Parabola--graph, equation and formula |Axis of Symmetry |Standard and Vertex Forms of Equation| real world applications | Converting between Standard and Vertex Forms | Tangent of Parabola| area of parabola Top |
