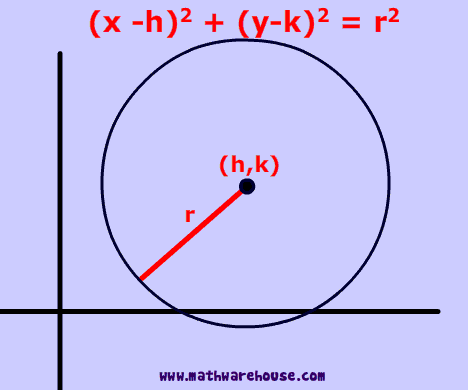
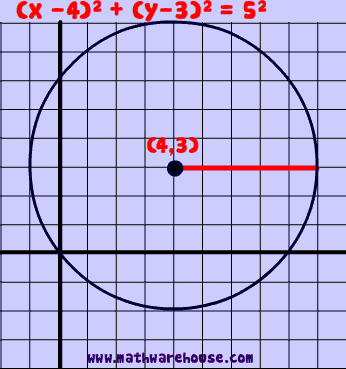
What is the standard form equaton of a circle?
Answer : is a way to express the definition of a circle on the coordinate plane.
The formula is $$(x -h)^2 + (y - k)^2 =r^2 $$.
Diagrams
Diagram 1
General Formula
Diagram 2
Circle with a center of (4,3) and a radius of 5
Another Example
Practice Problems
Practice 1
What is the equation of the circle pictured on the graph below?
Since the radius of this this circle is 1, and its center is the origin, this picture's equation is.
$$ (y-0)^2 + (x-0)^2 = 1^2 \\ y^2 + x^2 = 1 $$
Practice 2
Look at the graph below, can you express the equation of the circle in standard form?
Since the radius of this this circle is 1, and its center is (1, 0), this circle's equation is.
$$ (y-0)^2 +(x-1)^2 = 1^2 \\ y^2 + (x-1)^2 = 1 $$
Practice 3
Look at the graph below, can you express the equation of the circle in standard form?
Since the radius of this this circle is 2, and its center is (3,1) , this circle's equation is.
$$ (x-3)^2 +(y-1)^2 = 2^2 \\ (x-3)^2 +(y-1)^2 = 4 $$
Practice 4
What is the radius of the circles below?
Y2 + X2 = 9
$$ \sqrt{9} =3$$
Y2 + X2 = 16
$$ \sqrt{16} = 4$$
Y2 + X2 = 25
$$ \sqrt{ 25 } = 5 $$
Y2 + X2 = 11
$$ \sqrt{11}$$
Y2 + X2 = a
$$ \sqrt{a}$$
Practice 5
Look at each standard form equation below and identify the center and radius.
r = radius
(y - 3)2 + (x - 1)2 = 9
(1, 3) r = 3
(y - 5)2 + (x - 14)2 = 16
(14, 5) r = 4
(y - 1)2 + (x - 5)2 = 25
(5, 1) r = 5
(x + 2)2 + (y - 12)2 = 36
(-2, 12) r = 6
(y + 7)2 + (x + 5)2 = 49
(-5, -7) r = 7
(x + 8)2 + (y + 17)2 = 49
(-8, -17) r = 7
