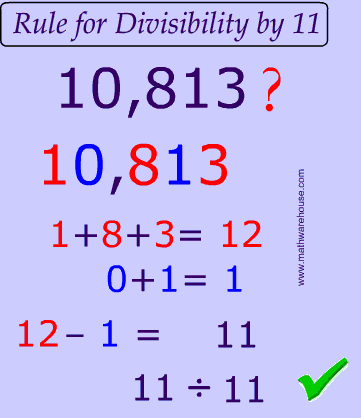What is the divisibility by 2 Rule?
Answer:Almost everyone is familiar with this rule, which states that any even number can be divided by 2.
Even numbers are multiples of 2. A number is even if it ends in 0, 2, 4, 6, or 8.
There are many shortcuts or tricks that allow you to test whether a number, or dividend, is divisible by a given divisor. This page focuses on the most-frequently studied divisibility rules which involve divisibility by
2,
3,
4,
5,
6,
8,
9,
10, and
by 11
Examples of numbers that are even and therefore pass this divisibility test.
| Number | Explanation |
| 12 | Since the last digit is a 2, the entire number, 12, is an even numberand therefore divisible by 2. |
| 318 | Since the last digit is an 8, this is an an even number and therefore divisible by 2. |
| -310 | Since the last digit is 0, this is an an even number and therefore divisible by 2. |
| -32,814 | Since the last digit is a 4, this is an even number and therefore divisible by 2. |
Check if any number is divisible by two. Type in any number that you want, and the calculator will use the rule for divisibility by 2 to explain the result.
See what the rule for divisibility by two has to say about the following number:
Examples of numbers that are do not pass this divisibility test because they are not even.
| Number | Explanation |
| 3 | 3 is not an even number. |
| 103 | Not an even number. |
| 157 | Not an even number. |
| 221 | Not an even number. |
What is the divisibility by 3 rule?
Answer:Rule: A number is divisible by 3 if the sum of its digits is divisible by 3.
375, for instance, is divisible by 3 since sum of its digits (3+7+5) is 15. And 15 is divisible by 3.
| Number | Explanation |
| 12 | $$ 1 + 2 = 3$$ and 3 is divisible by 3. |
| 36 | $$ 3 + 6 = 9 $$ and 9 is divisible by 3. |
| 102 | $$1 + 0 + 2 = 3$$ and 3 is divisible by 3. |
| 100,002,000 | $$ 100,002,000 = 1 + 0 + 0 + 0 + 0 + 2 + 0 + 0 + 0 = 3$$ and 3 is divisible by 3. |
| 36 | $$ 3 + 6 = 9 $$ and 9 is divisible by 3. |
Check if the following number: is evenly divisible by three.
| Number | Explanation |
| 14 | 1 + 4 = 5 and since 5 is not divisible by 3, so 14 is also not. |
| 124 | $$1 + 2 + 4 = 7$$ which is no good, since 7 is not evenly divisible by 3. |
| 100,002,001 | $$1 + 0 + 0 + 0 + 2 + 0 + 0 + 1 = 4$$ so this very large also does not pass this divisibility test. |
What is the divisibility by 4 rule?
Answer:Rule: A number is divisible by 4 if the number's last two digits are divisible by 4.
9,312, for instance, is divisible by 4 since its last 2 digits are 12. And 12 is divisible by 4.
Examples of numbers that are divisible by 4:
| Number | Explanation |
| 112 | Since the last two digits, 12, are divisible by 4, the number 112 is also divisible by 4. |
| 10,948 | The last two digits, 48, are divisible by 4. Therefore, the whole number is also. |
| 100,002,088 | Yep, this satisfies rule because 88 is divisible by 4! |
| -12,036 | 36 and 36 is evenly divided by 4, so -12,036 passes the test! |
See if the following is evenly divisible by four.
Examples of numbers that are do not pass this divisibility test.
| Number | Explanation |
| 113 | Since the last two digits, 13, are not divisible by 4, the whole number does not pass this divisibility test. |
| 10,941 | The last two digits, 41, are not de visible by 4. Therefore, the whole number does not satisfy the rule for 4. |
| 100,002,014 | Those last two digits, 14, do not work. |
| -1,011 | 11 is not divisible by 4, so 1,011 fails this test. |
Ever wonder why these rules work. The test for 4 makes sense if you just break down the numbers. Think about what this rule says: "All that matters is whether or not the last two digits are divisible by 4." Let's look at why this rule is true.
Examine some three digit numbers-
124 is the same as 100 + 24, and we know that 100 is divisible by 4 so all that matters here is whether or not 24, or the last two digits, are divisible by 4. The same could be said for any three digit number 224 = 200 + 24, and we know that 200 is divisible by 4 so again all that we're worried about are these last two digits.
- Any multiple of 100 is divisible by four! Whether you're talking about 300, 700, 1000, 1100, 123,000 -- All of these multiples of 100 are divisible by 4, which means that all that we ever have to worry about is the last two digits!
What is the divisibility by 5 rule?
Answer:Rule: A number is divisible by 5 if its last digit is a 0 or 5.
See what the rule for divisibility by five has to say about the following number:
Examples of numbers that are divisible by 5 and satisfy this rule
| Number | Explanation |
| 10 | Since the last digit is 0, this number is divisible by 5. |
| 15 | Since the last digit is 5, this number is divisible by 5. |
| -45 | Since the last digit is 5, this number is divisible by 5. |
Examples of numbers that are not divisible by 5.
| Number | Explanation |
| 11 | To be divisible by 5, the last digit must be 0 or 5. So 11 fails this test. |
| -19 | To be divisible by 5, the last digit must be 0 or 5. So -19 fails this test. |
What is the divisibility by 6 rule?
Answer:Since 6 is a multiple of 2 and 3, the rules for divisibility by 6 are a combination of the rule for 2 and the rule for 3.
In other words, a number passes this divisibility test only if it passes the testfor 2 and the for 3.
Rule: A number is divisible by 6 if it is even and if the sum of its digits is divisible by 3.
Examples of numbers that are divisible by 6.
| Number | Explanation |
| 114 | Therefore, 114 is divisible by 2 and by 3 ..so, yes , 114 is divisible by 6. |
| 241,122 | Therefore, 241,122 is divisible by 2 and by 3 ..so, yes, 241,122 is divisible by 6. |
See if the following number: is evenly divisible by six.
Examples of numbers that are do not pass this divisibility test.
| Number | Explanation |
| 207 | So, no, 204 is not divisible by 6. |
| 241,124 |
|
Divisibility by 8 Rule
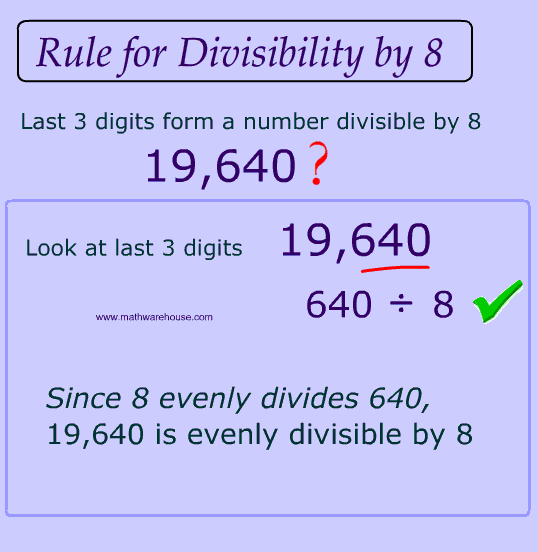
Rule A number passes the test for 8 if the last three digits form a number is divisible 8.
Examples of numbers that satisfy this rule and are divisible by 8.
| Number | Explanation |
| 9,640 | The last 3 digits, 640, are divisible by 8. Therefore, 9,640 is divisible 8 as well! |
| -77,184 | The last 3 digits , 184, are divisible by 8. Therefore, -77,184 is divisible 8 as well! |
| 20,233,322,496 | The last 3 digits, 496, are divisible by 8. Therefore , 20,233,322,496 is divisible 8 as well! |
See what the rule for divisibility by eight has to say about the following number:
Examples of numbers that are do not pass this divisibility test.
| Number | Explanation |
| 9,801 | Since last 3 digits are not divisible by 8, the entire number 9,801 is not. |
| -32,344,588 | Since last 3 digits are not divisible by 8, the entire number -32,344,588 is not. |
Divisibility by 9 Rule
Rule A number is divisible by 9 if the sum of the digits are evenly divisible by 9.
Examples of numbers that satisfy this rule and are divisible by 9.
| Number | Explanation |
| 4,518 | $$ 4 + 5 + 1 + 8 = 18$$ which is divisible by 9, so 4,518 is divisible by 9. |
| -6,993 | $$ 6 + 9 + 9 + 3 = 27 $$ which is divisible by 9 so, the entire number is divisible by 9. |
See if the following number: is evenly divisible by nine.
Examples of numbers that are do not pass this divisibility test.
| Number | Explanation |
| 6,992 | $$ 6 + 9 + 9 + 2 = 26 $$ which is not divisible by 9 so, the entire number is not divisible by 9. |
| 4,517 | $$ 4 + 5 + 1 + 7 = 17$$ which is not divisible by 9 so, the entire number is not divisible by 9. |
Divisibility by 10 Rule
Rule A number passes the test for 10 if its final digit is 0
Use the divisibility calculator below to determine if any number is divisible by ten. Type in any number that you want, and the calculator will use the rule for divisibility by 10 to explain the result.
Examples of numbers that are divisible by 10.
| Number | Explanation |
| 190 | Last digit is 0, that's all that is needed for a number to be divisible by 10. |
| -231,110 | Last digit is 0, that's all that is needed for a number to be divisible by 10. |
See what the rule for divisibility by ten has to say about the following number:
Examples of numbers that do not pass this divisibility test
| Number | Explanation |
| 31,205 | Since the last digit is not 0, this number is not divisible by 10. |
| -100,002 | Since the last digit is not 0, this number is not divisible by 10. |
Divisibility by 11 Rule
Rule A number passes the test for 11 if the difference of the sums of alternating digits is divisible by 11.(This abstract and confusing sounding rule is much clearer with a few examples).
Use the divisibility calculator below to determine if any number is divisible by eleven. Type in any number that you want, and the calculator will explain whether or not it's divisible by 11 based on this rule.
See if the following number: is evenly divisible by eleven.
Examples of numbers that satisfy this rule.
| Number | Explanation |
| 119,777,658 | $$ (1+ 9 + 7 + 6 + 8) - (1+ 7 + 7 + 5) = 31 - 20 = 11 $$ and since 11 is evenly divisible by 11, the entire number is also |
| 10,813 | $$ (1 + 8 + 3) - (0+1) = 12-1 = 11 $$ |
| 25,784 | $$ (2 + 7 + 4) - (5 + 8) = 13 - 13 = 0 $$ Yes, this does indeed work. In case you found this one, a bit confusing, remember that any number evenly divides 0. Think about it, how many 11's are there in 0? None, right. Well that means that 11 divides zero, zero times! |
Examples of numbers that do not pass this divisibility test.
| Number | Explanation |
| 10,823 | $$ (1+8+3) - (0+2) = 12- 2 =10 $$. No, no good. This one fails |
| 35,784 | $$ (3 + 7 + 4) - (5+8) = 14 - 13 = 1 $$ |
| 12,347, 496, 132 | $$ (1 + 3 + 7 + 9 + 3) - (2 + 4 + 4 + 6 + 3) = 23 - 19 = 4$$ |
A word of caution about Calculators and Large Numbers
Keep this in mind when you are using a calculator. Calculators lose their accuracy when they start dividing large numbers such as 12,347,496,132. Try to divide that large number by 11. If your calculator outputs that 12,347,496,132 is divisible by 11, your calculator IS WRONG (Look at the last example at the bottom for details). When you're dealing with exceedingly large numbers, you should rely, whenever possible, on the rules on this page rather than a computer that can only handle numbers up to a certain size..
