|
 
  
   
     
 |
Classify equations as relations, functions or one-to-one functionsRelated: : Functions and Relations Maths Revision - Quizzes to help revise many different maths topics
To classify an equation as a function will always depend whether or not the given equation can have more than 1 element in the domain for any given element in the range. Some giveways include
Practice Problems
Part I Remembering The look and Feel of Various Equation Types
Practice Problem One

Practice Problem two
y = x +1 is a function because every element in the domain has onely 1 element in the range (which is 1 greater than said element in domain). Additionally, if you graph this equation you can see that it passes the vertical line test. 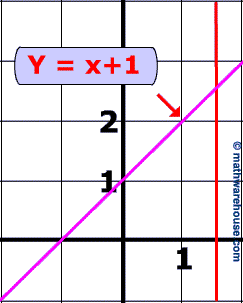 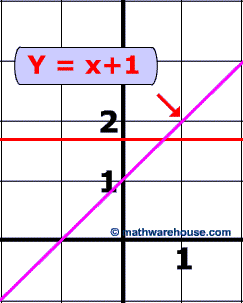
Practice Problem three
Is y - 5x = 1, a relation or a function? If so, is it a one-to-one function?
This line is a one to one function. In fact, all non-vertical and non-horizontal lines are one to one functions.
Practice Problem four
This equation can be rewritten as a the equation of a line as follows: . 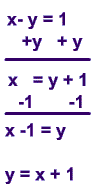
This equation is a line and since the line is not vertical or horizontal it is a 1-to-1 function. This line is a 1-to-1 function. In fact, all non-vertical and non-horizontal lines are 1-to-1 functions.
Practice Problem five
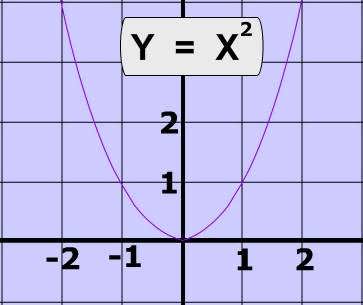
This is not a function because every element of the domain corresponds with two elements in the range. Consider for example two points on this equation (4,2) and ( 4,-2).
Practice Problem six
This is a function becuase every element of the domain corresponds with one element in the range; however, this is not a one-to-one funciton elements in the range correspond with two elements in the domain. Consider for example two points on this equation (3, 9) and ( -3, 9).
Practice Problem Seven
a function, a one-to-one function or just a relation?
(X – 5)² + (Y – 3 )² = 25 is the standard form equation of a circle.
Practice Problem Eight
a function, a one-to-one function or just a relation?
X² + (Y + 4 )² = 25 is the standard form equation of a circle.
Part II Quiz and Practice: Classify Relations
Practice Problem One
Is y = 3x + 1 a function , a 1 to 1 function or just a relation?
Since it is neither a vertical line such as x= 2 or a horizontal line such as y = 3, this is a one to one function. Practice Problem Two
Is y -2x = 1 a function , a 1 to 1 function or just a relation?
It can be rewritten as y = 2x + 1 Since it is neither a vertical line such as x= 2 or a horizontal line such as y = 3, this is a one to one function. Every element in the range and the domain have one and only one element. Practice Problem three
Is y -2x = 1 a function , a 1 to 1 function or just a relation?
It can be rewritten as y = 2x + 1 Since it is neither a vertical line such as x= 2 or a horizontal line such as y = 3, this is a one to one function. Every element in the range and the domain have one and only one element. Practice Problem Four
Is X² + y² = 25 a function , a 1 to 1 function or just a relation?
A circle does not pass the horizontal line test and it does not pass the vertical line test Therefore, this equation represents a relation (in fact all circles are relations and not functions, assumign there is no restriction on the domain and range. Practice Problem Five
Is y = 5 a function , a 1 to 1 function or just a relation?
Practice Problem Six
Is Y = X² + 2X+ 25 a function, a one-to-one function or just a relation?
This Page: Part I: Review of various equation types | Part II Practice quiz- classify relations as functions, 1-to-1 or neither Related: Related: : Functions in math|Interative Relation|Evaluating Functions|Vertical Line Test | Composition of functions | One to One Function|inverse of a function |Quiz on Classifying relations |