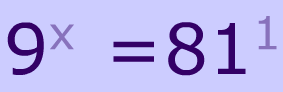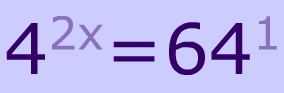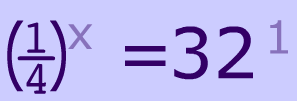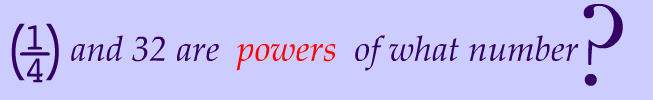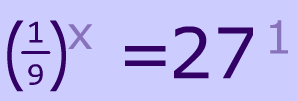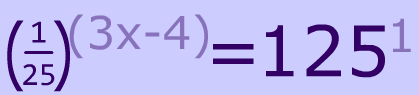$$ 2^{\red x} = 4 \\ 8^{\red{2x}} = 16 \\ \\ 16^{\red { x+1}} = 256 \\ \left( \frac{1}{2} \right)^{\red { x+1}} = 512 $$
As you might've noticed, an exponential equation is just a special type of equation. It's an equation that has exponents that are $$ \red{ variables}$$.
There are different kinds of exponential equations. We will focus on exponential equations that have a single term on both sides. These equations can be classified into 2 types.
$$ 4^x = 4^9 $$.
$$ 4^3 = 2^x $$.
$$ \left( \frac{1}{4} \right)^x = 32 $$ (Part II below)
Solve: $$ 4^{x+1} = 4^9 $$
Step 1Ignore the bases, and simply set the exponents equal to each other
$$ x + 1 = 9 $$
Step 2Solve for the variable
$$ x = 9 - 1 \\ x = \fbox { 8 } $$
CheckWe can verify that our answer is correct by substituting our value back into the original equation . .
$$
4^{x+1} = 4^9
\\
4^{\red{8}+1} = 4^9
$$
$$
4^{\red{9} } = 4^9
$$
Enter any exponential equation into the algebra solver below :
$$
\red 4^3 = \red 2^x
$$
$$
\red 9^x = \red { 81 }
$$
$$
\left( \red{\frac{1}{2}} \right)^{ x+1} = \red 4^3
$$
$$
\red 4^{2x} +1 = \red { 65 }
$$
In each of these equations, the base is different. Our goal will be to rewrite both sides of the equation so that the base is the same.
Solve: $$ 4^{3} = 2^x $$
Step 1Forget about the exponents for a minute and focus on the bases:
Rewrite the bases as powers of a common base. Do this by asking yourself :
Answer: They are both powers of 2
Rewrite equation so that both exponential expressions use the same base
$$ \red 4^{3} = 2^x \\ (\red {2^2})^{3} = 2^x $$
Use exponents laws to simplify
$$ (\red {2^2})^{3} = 2^x \\ (2^\red {2 \cdot 3 }) = 2^x \\ (2^\red 6 ) = 2^x $$
Solve like an exponential equation of like bases
$$ (2^\red 6 ) = 2^x \\ x = \fbox{6} $$
Substitute $$\red 6 $$ into the original equation to verify our work.
$$
4^{3} = 2^{\red 6}
$$
$$
64 = 64
$$
Unlike bases often involve negative or fractional bases like the example below. We are going to treat these problems like any other exponential equation with different bases--by converting the bases to be the same.
Forget about the exponents for a minute and focus on the bases:
Rewrite the bases as powers of a common base. Ask yourself :
You can use either 3 or 9. I will use 9.
$ \\ 81 = \red 9 ^{\blue 2} \\ 9 = \red 9 ^{\blue 1} \\ $
Substitute the rewritten bases into original equation
$$ (\red 9^{\blue 1})^x = \red 9^{\blue 2} $$
Use exponents laws to simplify
$$ (\red 9^{\blue 1})^x = \red 9^{\blue 2} \\ 9^{1 \cdot x } = 9 ^{2} \\ 9^{x } = 9 ^{2} $$
Solve like an exponential equation of like bases
$$ x = 2 $$
Rewrite this equation so that it looks like the other ones we solved. Isolate the exponential expression as follows:
$$ 4^{2x} +1 \red{-1} = 65\red{-1} \\ 4^{2x} = 64 $$
Forget about the exponents for a minute and focus on the bases:
Rewrite the bases as powers of a common base. Ask yourself :
They are both powers of 2 and of 4. You could use either base to solve this. I will use base 4
$ \\ 64 = \red 4 ^{\blue 3} \\ 4 = \red 4 ^{\blue 1} \\ $
Substitute the rewritten bases into original equation
$$ 4^{2x} = 64 \\ \red 4^{\blue{ 2x }} = \red 4^{\blue 3 } $$
Use exponents laws to simplify
$$ \red 4^{\blue{ 2x }} = \red 4^{\blue 3 } $$
Not much to do this time :)
Solve like an exponential equation of like bases
$$ 2x = 3 \\ x = \frac{3}{2} $$
Since these equations have different bases, follow the steps for unlike bases
Forget about the exponents for a minute and focus on the bases:
Rewrite the bases as powers of a common base. Ask yourself :
They are both powers of 2
$ \\ 32 = \red 2 ^{\blue 5} \\ \frac 1 4 = \red 2 ^{\blue {-2}} \\ $
Rewrite as a negative exponent and substitute the rewritten bases into original equation
$$ \left( \frac{1}{4} \right)^x = 32 \\ \left( \frac{1}{2^2} \right)^x = 32 \\ \left(\red 2 ^{\blue{-2}} \right)^x = \red 2^{\blue 5} $$
Use exponents laws to simplify
$$ \left(\red 2 ^{\blue{-2}} \right)^x = \red 2^{\blue 5} \\ 2 ^{-2 \cdot x} = 2^5 \\ 2 ^{-2x} = 2^5 $$
Solve like an exponential equation of like bases
$$ 2 ^{-2x} = 2^5 \\ -2x = 5 \\ \frac{-2x}{-2} = \frac{5}{-2} \\ x = -\frac{5}{2} $$
Rewrite this equation so that it looks like the other ones we solved. Isolate the exponential expression as follows:
$$ \left( \frac{1}{9} \right)^x -3 \red{+3} =24\red{+3} \\ \left( \frac{1}{9} \right)^x=27 $$
Forget about the exponents for a minute and focus on the bases:
Rewrite the bases as powers of a common base. Ask yourself :
They are both powers of 3.
$ \\ \frac 1 9 = \red 3 ^{\blue {-2}} \\ 27 = \red 3 ^{\blue 3} \\ $
Rewrite as a negative exponent and substitute into original equation
$$ \left( \frac{1}{9} \right)^x=27 \\ \left( \red{3^{-2}}\right)^x=\red{3^3 } $$
Use exponents laws to simplify
$$ 3^\red{{-2 \cdot x}} = 3^3 \\ 3^\red{{-2x}} = 3^3 $$
Solve like an exponential equation of like bases
$$ -2x = 3 \\ x = \frac{3}{-2} \\ x = -\frac{3}{2} $$
Rewrite this equation so that it looks like the other ones we solved--In other words, isolate the exponential expression as follows:
$$ \left( \frac{1}{25} \right)^{(3x -4)} -1 \red{+1} = 124 \red{+1} \\ \left( \frac{1}{25} \right)^{(3x -4)} = 125 $$
Forget about the exponents for a minute and focus on the bases:
Rewrite the bases as powers of a common base. Ask yourself :
They are both powers of 5.
$ \\ \frac { 1 } { 25 } = \red 5 ^{\blue {-2}} \\ 125 = \red 5 ^{\blue 3} \\ $
Rewrite as a negative exponent and substitute into original equation
$$ \left( \frac{1}{25} \right)^{(3x -4)} = 125 \\ \left( \red{5^{-2}} \right)^{(3x -4)} = \red{5^3} $$
Use exponents laws to simplify
$$ 5^\red{{-2 \cdot (3x -4)}} = 5^3 \\ 5^\red{{(-6x + 8)}} = 5^3 $$
Solve like an exponential equation of like bases
$$ -6x + 8 =3 \\ -6x = -5 \\ x = \frac{-5}{-6} \\ x = \frac{5}{6} $$
