 

 
 |
Definition of Real Numbers
Properties, Examples, and Non Examples
A Real Definition :
The definition in math text books of real numbers is often not helpful to the average person who is trying to gain an introductory and intuitive sense of what a real number.
Real numbers are just the numbers on the number line.
It is the easiest way to think of them. Basically, if you can put the number in question on an infinitely big number line, then it is a real number. Also, you have to be add ,subtract ,multiply, divide that number in a way that is consistent with the number line. They include many types of numbers:
Types of Real Numbers with examples
- Rational Numbers -- in other words all integers , fractions
and decimals (including repeating decimals)
- Irrational Numbers
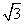 , , 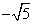 , yes, irrational numbers can be ordered and put on a number line, we know that , yes, irrational numbers can be ordered and put on a number line, we know that 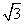 comes before comes before 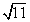
Properties of Real Numbers
- Real numbers can be ordered (this is not true, for instance, of imaginary numbers )
- They can be added, subtracted , multiplied and divided by nonzero numbers in an ordered way. So what does that mean? Basically it means that
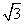 comes before comes before 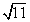 on the number line and that they both come before on the number line and that they both come before 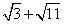 . We know that this fact is true for rational and irrational numbers. Think about the rational numbers 3 and 5, we know that we can order 3 and 5 as follows. 3 comes before 5 and both numbers come before 8(3+5) . . We know that this fact is true for rational and irrational numbers. Think about the rational numbers 3 and 5, we know that we can order 3 and 5 as follows. 3 comes before 5 and both numbers come before 8(3+5) .
What about numbers that are not Real ?
The first type of non-real number that students usually learn is imaginary numbers. These numbers cannot be ordered on a number line like the real numbers can be.
|






