Unfortunately, in the last year, adblock has now begun disabling almost all images from loading on our site, which has lead to mathwarehouse becoming unusable for adlbock users.
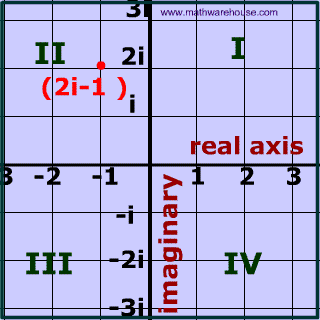
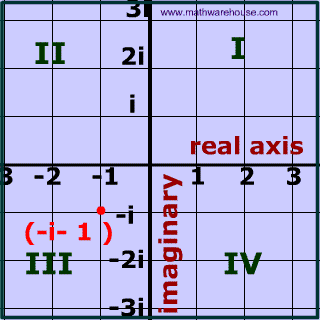
Overview: This article covers the definition of complex numbers of the form $$ a+ bi $$ and how to graph complex numbers.
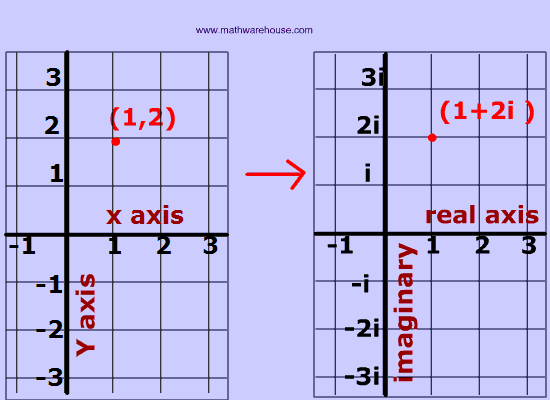
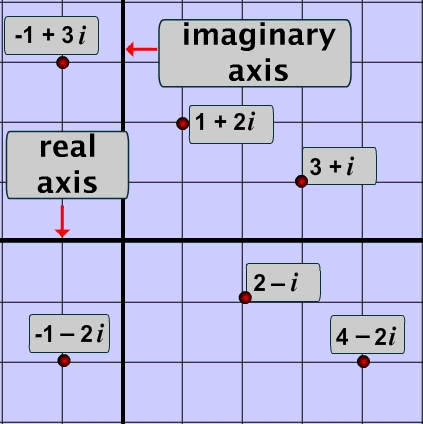
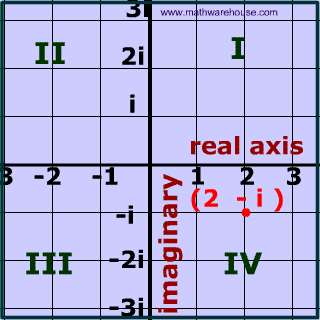
A complex number can be written in the form a + bi where a and b are real numbers (including 0) and i is an imaginary number.
Therefore a complex number contains two 'parts':
note: Even though complex have an imaginary part, there are actually many real life applications of these "imaginary" numbers including oscillating springs and electronics.
$$ \begin{array}{c|c} \blue 3 + \red 5 i & \\\hline \blue{12} + \red{\sqrt{-3}} & \red{\sqrt{-3}} \text{ is the } \blue{imaginary} \text{ part} \\\hline \blue 9 - \red i & \\\hline \blue{12} - \red{\sqrt{-25}} & \red{\sqrt{-25}} \text{ is the } \blue{imaginary} \text{ part} \\\hline \end{array} $$
Complex numbers are often represented on a complex number plane (which looks very similar to a Cartesian plane).
This complex number is in the fourth quadrant.
This complex number is in the 2nd quadrant.
This complex number is in the 3rd quadrant.
