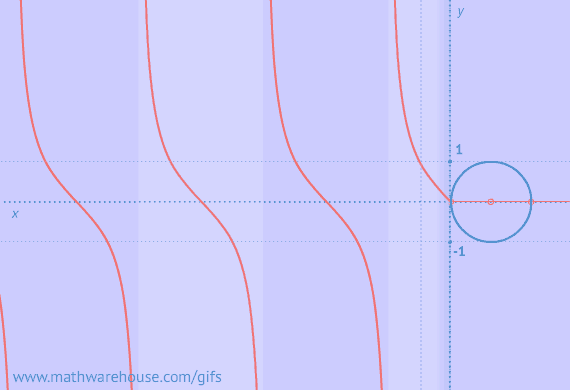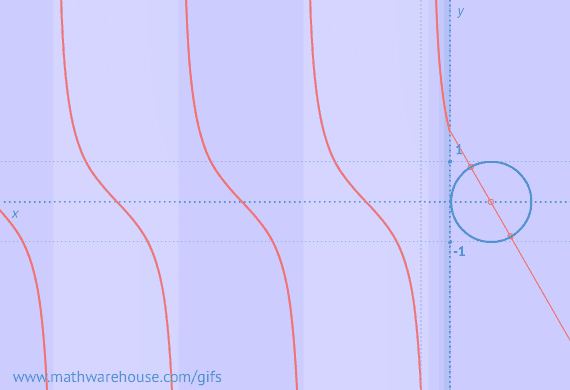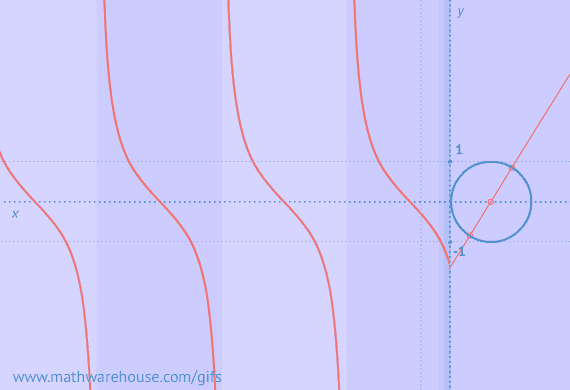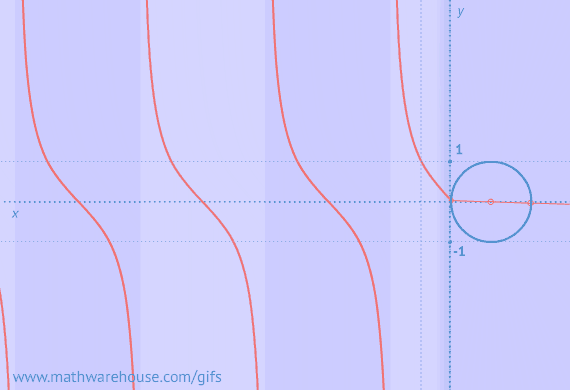
Example of Zero Triangles Possible
Use the Law of Sines to solve for $$m \angle A$$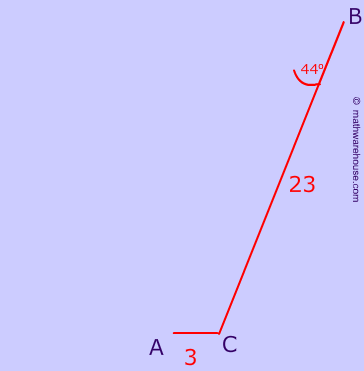
$$ BC = 23 \\ AC = 3 \\ \angle B = 44^{\circ}$$.
$ \frac{sin( A)}{ 23 } = \frac{sin(44)}{3} \\ sin( A) = \frac{23 \cdot sin(44)}{3} \\ sin( A) = \red { 5.32571417} \\ \boxed{\text{ No Solution}} $
As you can see $$ \angle A $$ is 'impossible' because the sine of an angle cannot be equal to 5.3. (Remember the greatest value that the sine of an angle can have is 1)
Visual of Zero Triangles Possible
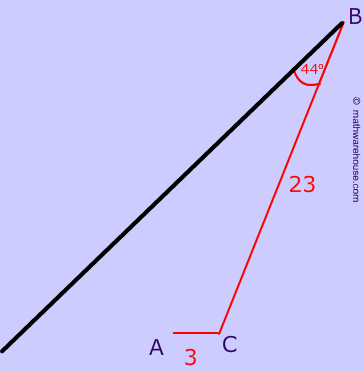
There is no way to do it
Example 1
For $$\triangle ABC$$, $$ a = 6, b =10$$, and $$m \angle A = 42^{\circ}$$. How many Triangles can be formed?
Work
$$ \frac{sin ( B )}{b} = \frac{sin ( A )}{a} \\ \frac{sin (\red B)}{10} = \frac{sin (42^{\circ})}{6} \\ sin(\red B)= \frac{10 \cdot sin (42^{\circ})}{6} \\ sin(\red B)= 1.11522 \\ \boxed{\text{No Solution}} $$
Answer:
Zero Triangles . The maximum value of the sine function is 1.
$$ sin(B)= \cancel {\red {1.11522}} $$(from our free downloadable worksheet )
Practice Problem
Work
$$ \frac{sin ( E )}{e} = \frac{sin ( F )}{f} \\ \frac{sin (\red E)}{27} = \frac{sin (37^{\circ})}{12} \\ sin(\red E)= \frac{27 \cdot sin (37^{\circ})}{12} \\ sin(\red B)= 1.3541 \\ \boxed{\text{No Solution}} $$
Answer:
There is no possible $$\angle E $$ with the given dimensions . The maximum value of the sine function is 1.
$$ sin(B)= \cancel {\red {1.3541}} $$(from our free downloadable worksheet )