How to Rotate a Point in Math. Interactive demonstration and picture of common rotations (90,180,270 and 360)

Rotations are Direct Isometries

Rotation notation is usually denoted R(_{center , degrees})

"Center" is the 'center of rotation.' This is the point around which you are performing your mathematical rotation.
"Degrees" stands for how many degrees you should rotate. A positive number usually by convention means counter clockwise.

A rotation is a direct isometry , which means that both the distance and orientation are preserved.

As you can see in diagram 1 below, triangle $$ \triangle ABC $$ is rotated by $$90^{\circ}$$ to its image $$ \triangle A'B'C' $$. And the distance between each of the vertices of the preimage is maintained in its image.

Diagram 1

$ m \overline{AB} = 4 \\ m \overline{A'B'} = 4 \\ \\ m \overline{BC} = 5 \\ m \overline{B'C'} = 5 \\ \\ m \overline{CA} = 3 \\ m \overline{C'A'} = 3 $

You can also see that the orientation of the letters is preserved, i.e. that the vertices in the original shape are ordered $$ABC$$ , in clockwise order, and that the image maintains the same clockwise order, making rotations a direct isometry.

Diagram 2

How to Rotate a Point

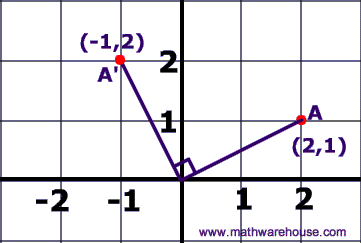
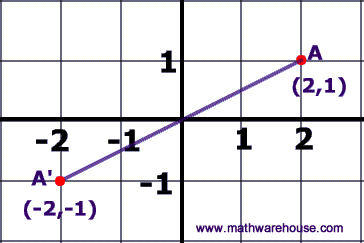
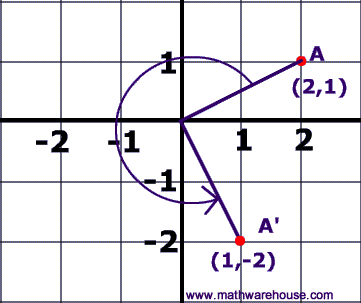
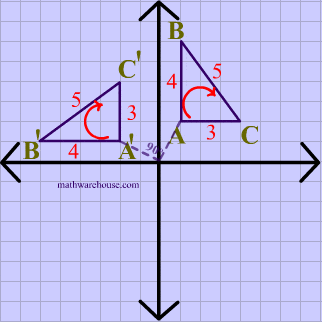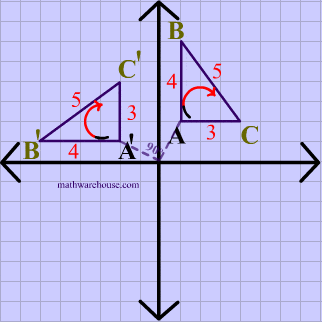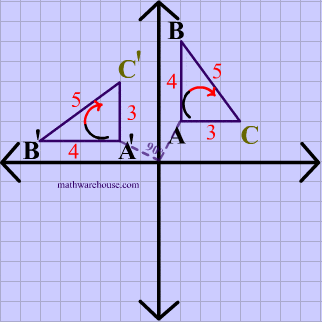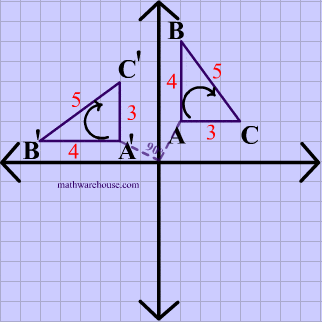
The demonstration below that shows you how to easily perform the common Rotations (ie rotation by 90 , 180 , or rotation by 270) . There is a neat 'trick' to doing these kinds of transformations. The basics steps are to graph the original point (the pre-image), then physically 'rotate' your graph paper, the new location of your point represents the coordinates of the image. It's much easier to understand these steps if you watch the visual demonstration below.

Plot the original point on graph paper

Turn or 'rotate' your graph paper by the amount you are asked to rotate : °

Label the new Coordinates the cordinates of the image!

Snap to grid

You can drag the point anywhere you want

How To Perform Rotations The Easy Way (Mouse Over To Start)

Examples of the Most Common Rotations

Rotation by 90° about the origin: R_{(origin, 90°)}

A rotation by 90° about the origin can be seen in the picture below in which A is rotated to its image A'. The general rule for a rotation by 90° about the origin is (A,B) (-B, A)

picture of rotation by 90 degrees about origin

Rotation by 180° about the origin: R_{(origin, 180°)}

A rotation by 180° about the origin can be seen in the picture below in which A is rotated to its image A'. The general rule for a rotation by 180° about the origin is (A,B) (-A, -B)

picture of rotation by 180 degrees about origin

Rotation by 270° about the origin: R_{(origin, 270°)}

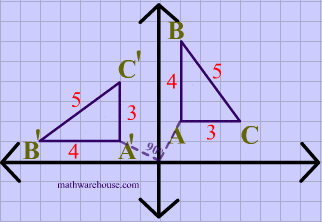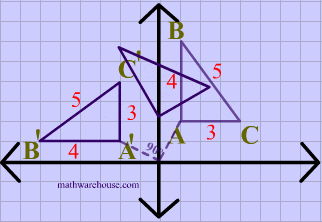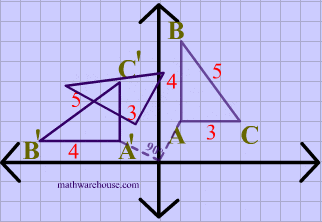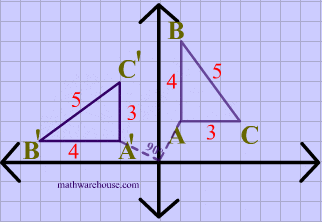
A rotation by 270° about the origin can be seen in the picture below in which A is rotated to its image A'. The general rule for a rotation by 270° about the origin is (A,B) (B, -A)