Point Reflections, Formula and Examples explained with applet, examples and practice problems. Center at origin and at any arbitrary point

Formula for Point Reflection over Origin

A point reflection is just a type of reflection. In standard reflections, we reflect over a line, like the y-axis or the x-axis. For a point reflection, we actually reflect over a specific point, usually that point is the origin .

$ \text{Formula} \\ r_{(origin)} \\ (a,b) \rightarrow ( \red -a , \red -b) $

Example 1

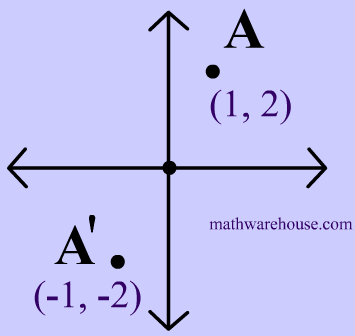
$ r_{origin} (1,2) = (\red -1 , \red -2) $

Example 2

$ r_{origin} (3,4) = (\red -3 , \red -4) $

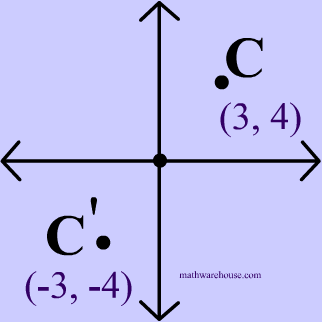
Eample 2 shows the same reflection over origin .

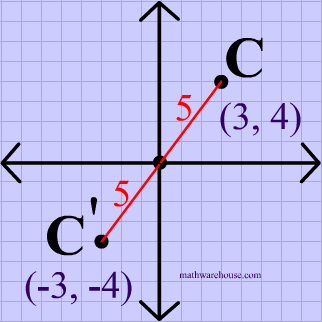
Distance to point of reflection

The distance from the preimage to the point of reflection is equal to the distance from the point of reflection to the image .

Example 3

Example 4

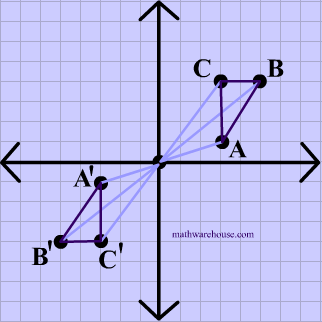
A graph showing a triangle's shape reflected over the origin. The distance from each vertex (and actually each and every single point ) of the preimage to the origin is equal to distance between the origin and each point of the image .

Example 5

The origin might be the most common point of reflection, but you can use any point. And the same rules apply. The diagram below uses the point $$(1,2)$$ as the point of reflection.

The the distances between each point on the preimage and the point of reflection $$ (1,2)$$ are equal to the distances between $$(1,2)$$ and each point on the image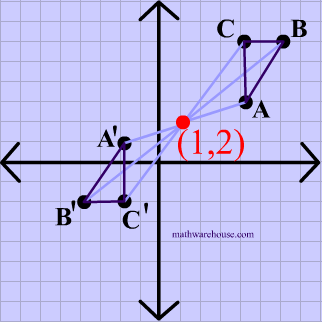

Practice problems like example 5 here.

Interactive applet for Point Reflection over Point

Show Distance

Auto Flip

Snap to grid

Select Shape To reflect

You can drag point of reflection

You can drag around the point to reflect

Practice Problems I

Problem 1

Reflect the point $$ (2,3)$$ over the origin.

Remember the formula for reflecting over the origin is to just to negate the signs of both coordinates.

Problem 2

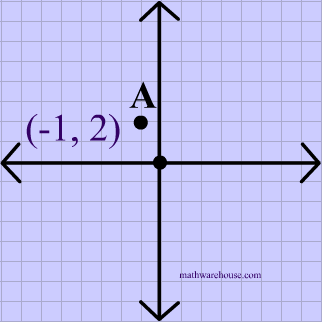
Reflect the point $$ (-1,2)$$ over the origin.

Remember the formula for reflecting over the origin is to just to negate the signs of both coordinates.

$ r_{origin} (-1, 2) \\ (-1, 2) \rightarrow (\red - -1, \red- 2 ) \\ \boxed{ (1,-2 ) } $

Problem 3

Reflect the point $$ (3, -4 )$$ over the origin.

$ r_{origin} (3, -4) \\ (3, -4) \rightarrow (\red -3, \red- -4) \\ \boxed{ (-3,4) } $

Practice Problems II

These practice problems involve reflections over a point that is not the origin like example 5 above.

Problem 2.1

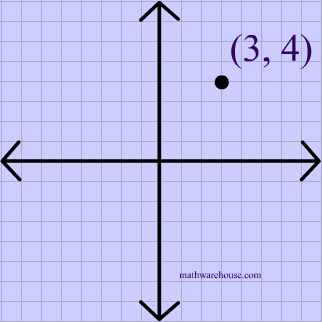
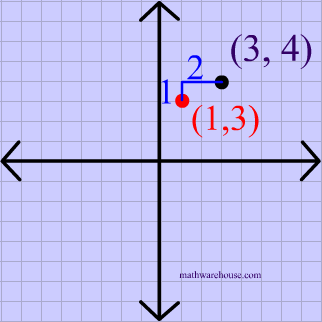
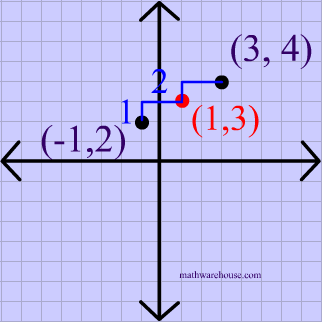
Reflect the point $$ (3,4 )$$ over the point $$ \red { ( 1, 3 )} $$.

There is no simple formula for a reflection over a point like this, but we can follow the 3 steps below to solve this type of question.

First, plot the point of reflection, as shown below.

Second, similar to finding the slope, count the number of units down and over from the preimage to the point of reflection.

Third, repeat step 2 and again count the same number of units down and over and you've now found where the image should be graphed which is the point $$ (-1, 2) $$ .

Problem 2.2

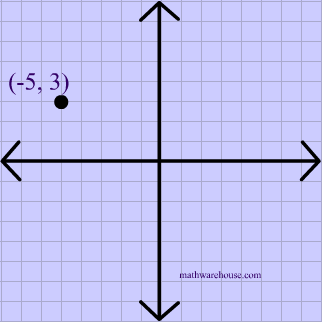
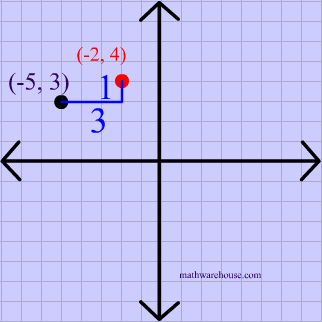
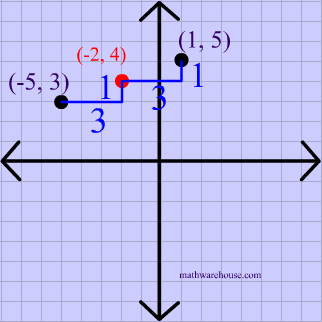
Reflect the point $$ (-5,3 )$$ over the point $$ \red { ( -2, 4 )} $$.

There is no simple formula for a reflection over a point like this, but we can follow the 3 steps below to solve this type of question.

First, plot the point of reflection, as shown below.

Second, similar to finding the slope, count the number of units up and over from the preimage to the point of reflection.

Third, repeat step 2 and again count the same number of units down and over and you've now found where the image should be graphed which is the point $$ (1, 5) $$ .