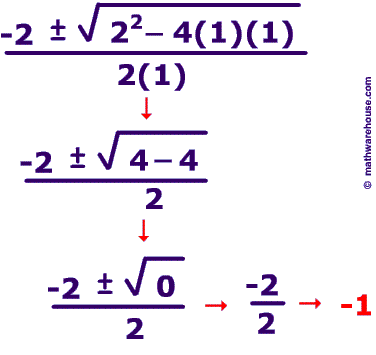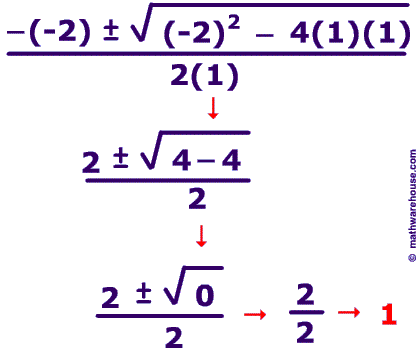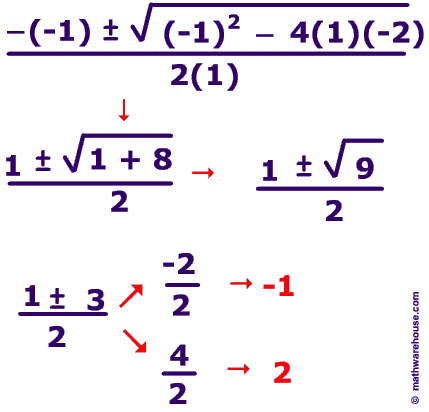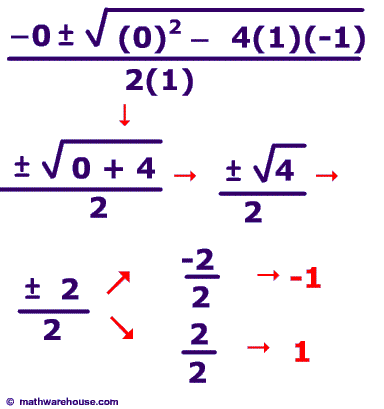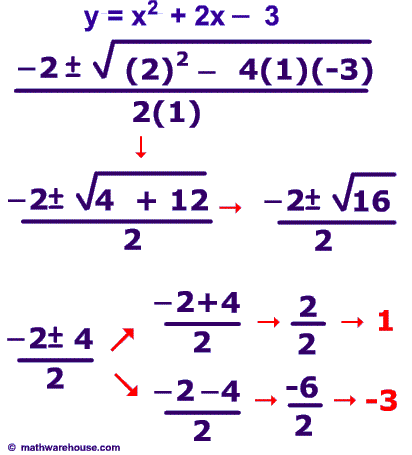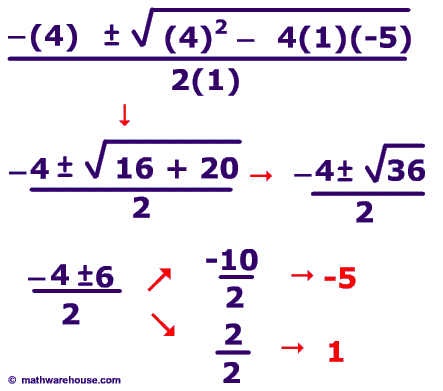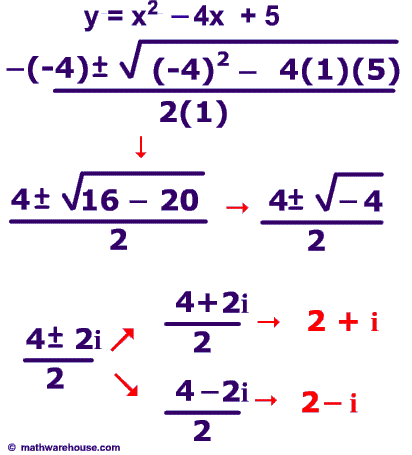What is the Quadratic Formula?
The quadratic formula is:
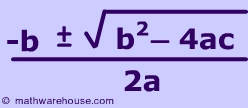
What it is, what it does, and how to use it
The quadratic formula is:
The quadratic formula calculates the solutions of any quadratic equation.
A quadratic equation is an equation that can be written as ax ² + bx + c where a ≠ 0. In other words, a quadratic equation must have a squared term as its highest power.
$$ y = 5x^2 + 2x + 5 \\ y = 11x^2 + 22 \\ y = x^2 - 4x +5 \\ y = -x^2 + + 5 $$
$$ y = 11x + 22 \\ y = x^3 -x^2 +5x +5 \\ y = 2x^3 -4x^2 \\ y = -x^4 + 5 $$
Well a solution can be thought in two ways:
| Algebra: |
For any quadratic equation of the form f(x) = ax2+bx+c, the solution is when f(x) = 0. |
| Geometry |
The solution is where the graph of a quadratic equation (a parabola) is intersects the x-axis. 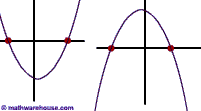
This, of course, only applies to real solutions. |
Use the formula to solve theQuadratic Equation: $$ y = x^2 + 2x + 1 $$.
Just substitute a,b, and c into the general formula:
$$ a = 1 \\ b = 2 \\ c = 1 $$
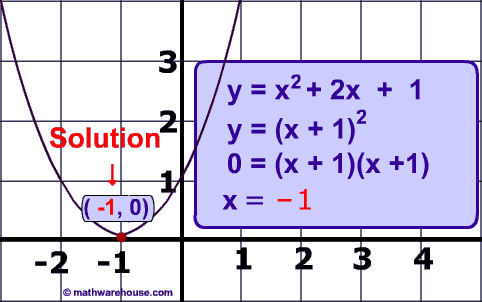
Below is a picture representing the graph of y = x² + 2x + 1 and its solution.
A catchy way to remember the quadratic formula is this song (pop goes the weasel).
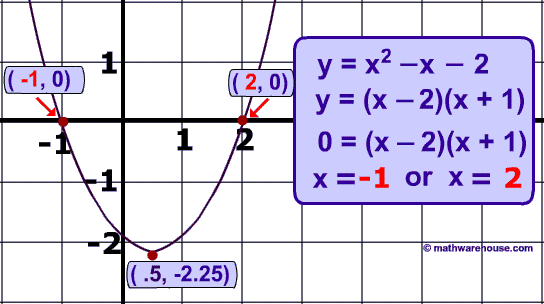
In this quadratic equation,y = x² − x − 2 and its solution:
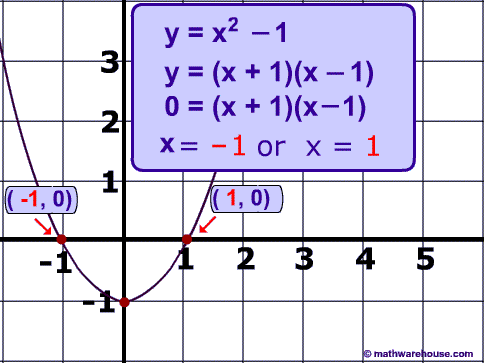
In this quadratic equation, y = x² − 1 and its solution:
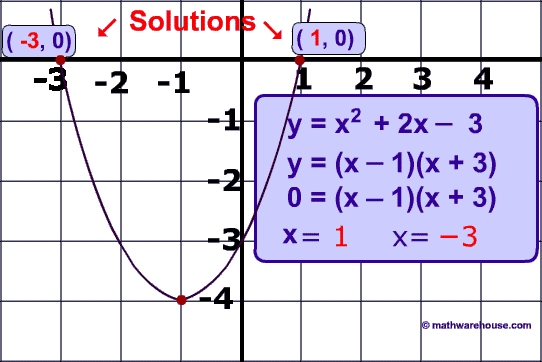
In this quadratic equation, y = x² + 2x − 3 and its solution:
Below is a picture of the graph of the quadratic equation and its two solutions.
In this quadratic equation, y = x² + 4x − 5 and its solution:
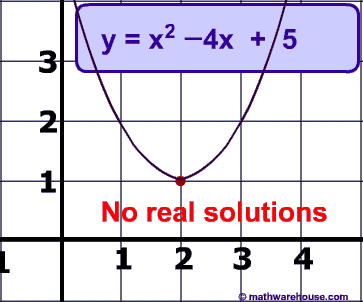
In this quadratic equation,y = x² − 4x + 5 and its solution:
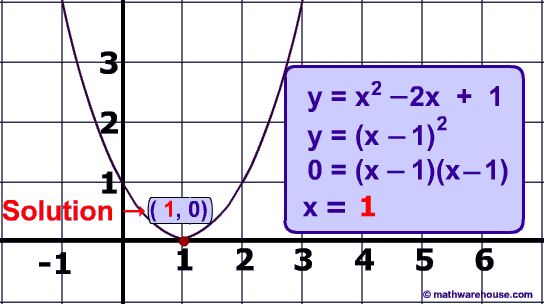
Below is a picture of this quadratic's graph.