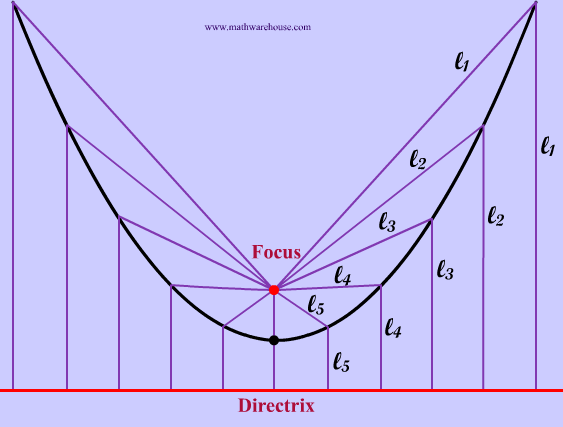
A parabola is a locus of points equidistant from both 1) a single point, called the focus of the parabola, and 2) a line, called the directrix of the parabola.
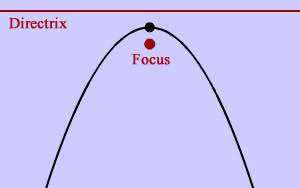
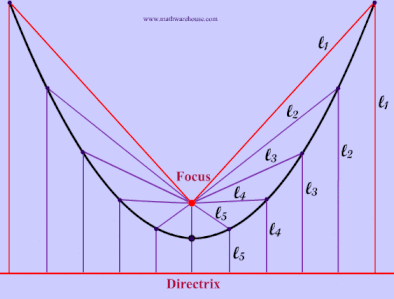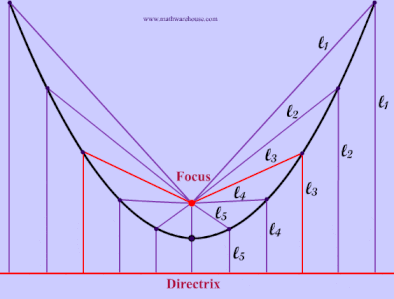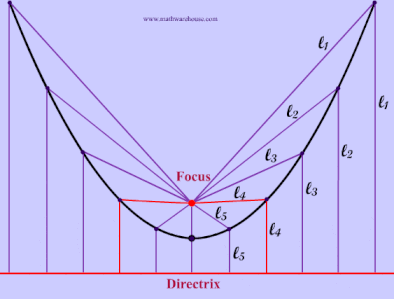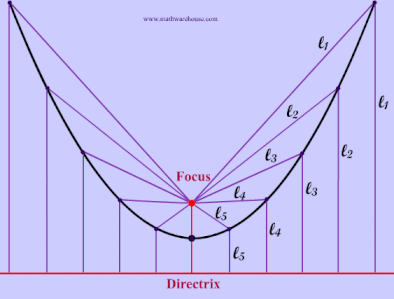
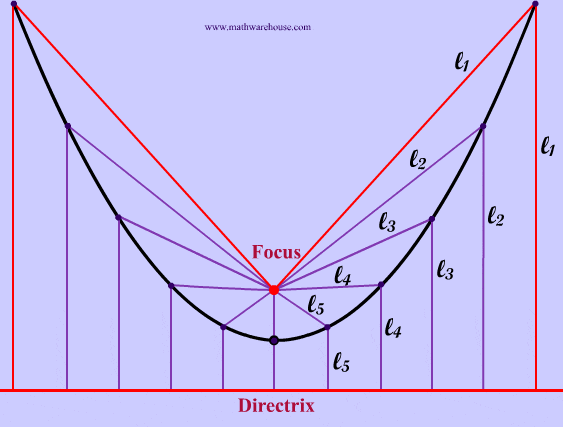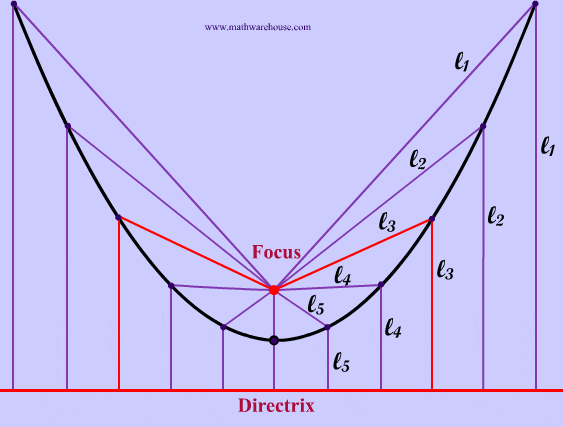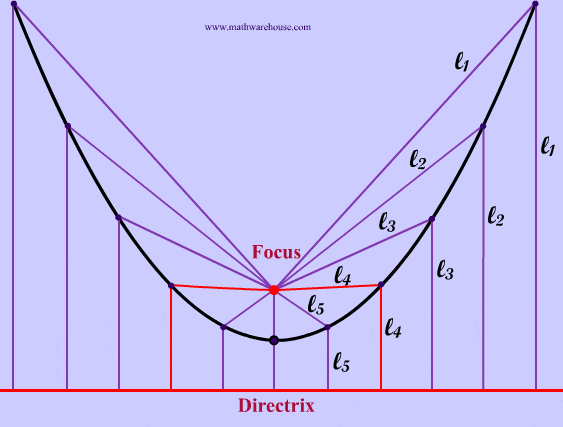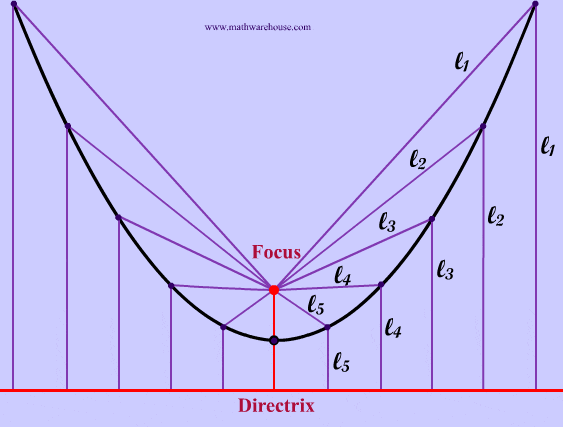
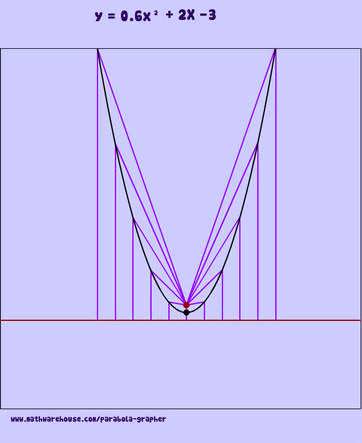
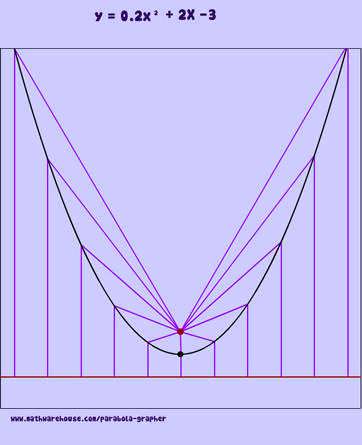
The red point in the pictures below is the focus of the parabola and the red line is the directrix. As you can see from the diagrams, when the focus is above the directrix Example 1, the parabola opens upwards. In the next section, we will explain how the focus and directrix relate to the actual parabola. Explore this more with our interactive app below.
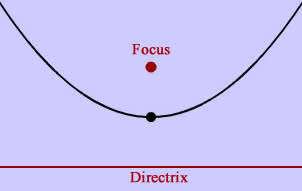
When the focus is below, the directrix , then the parabola opens downwards.
The purple lines in the picture below represent the distance between the focus and different points on the directrix . Every point on the parabola is just as far away (equidistant) from the directrix and the focus.
In other words, line $$ l_1 $$ from the directrix to the parabola is the same length as $$ l_1 $$ from the parabola back to the focus . The same goes for all of the other distances from a point on the parabola to the focus and directrix ( $$ l_2, l_3 \text{ etc.. } $$). See animation below
You probably know that the smaller |a| in the standard form equation of a parabola, the wider the parabola. In other words y = .1x² is a wider parabola than y = .2x² and y = -.1x² is a wider parabola than y = .-2x². You can understand this 'widening' effect in terms of the focus and directrix. As the distance between the focus and directrix increases, |a| decreases which means the parabola widens. See the pictures below to understand.
|a| = 1
|a| = .6
|a| =.3
|a| = .2
Explore how the focus and directrix relate to the graph of a parabola with the interactive program below.
