What are similar triangles?
Answer: Similar triangles have the same 'shape' but are just scaled differently. Similar triangles have congruent angles and proportional sides.
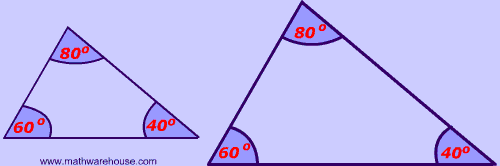
What is true about the angles of similar triangles?
Answer: They are congruent. as the picture below demonstrates.
What is true about the sides of similar triangles?
Answer: Corresponding sides of similar triangles are proportional. The example below shows two triangle's with their proportional sides ..
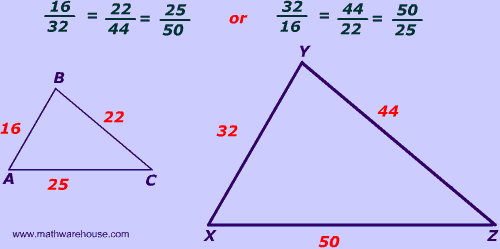
What is the similarity ratio (aka scale factor)?
Answer: It's the ratio between corresponding sides. In the picture above, the larger triangle's sides are two times the smaller triangles sides so the scale factor is 2
$$ 16 \cdot 2 = 32 \\ 22 \cdot 2 = 44 \\ 25 \cdot 2 = 50 $$
Notation: $$ \triangle ABC $$~$$\triangle XYZ $$ means that "$$ \triangle ABC \text{ is similar to } \triangle XYZ $$"
How do you find the similarity ratio?
Answer: Match up any pair of corresponding sides and set up a ratio. That's it!
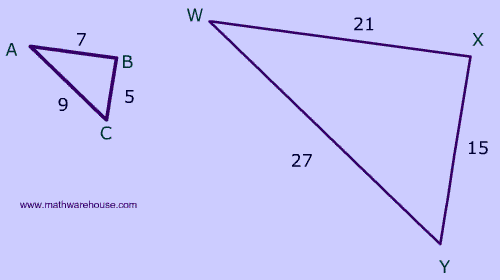
If $$ \triangle ABC $$ ~ $$ \triangle WXY $$, then what is the similarity ratio?
Step 1Pick a pair of corresponding sides
(follow the letters)
AB and WX are corresponding.
Follow the letters: $$ \triangle \color{red}{AB}C$$ ~ $$\triangle \color{red}{WX}Y$$
Substitute side lengths into proportion
$$ \frac{AB}{WX} = \frac{7}{21} $$
Simplify (if necessary)
$$ \frac{7}{21}=\frac{1}{3} $$
Why is the following problem unsolvable?
If $$ \triangle $$ JKL ~ $$\triangle $$ XYZ, LJ = 22 ,JK = 20 and YZ = 30, what is the similarity ratio?
Answer: You are not given a single pair of corresponding sides so you cannot find the similarity ratio.
Remember: How to Find corresponding sides
Corresponding sides follow the same letter order as the triangle name so:
- YZ of $$ \triangle X\color{red}{YZ}$$ corresponds with side KL of$$\triangle J\color{red}{KL} $$
- JK of $$ \triangle \color{red}{JK}L $$ corresponds with side XY of$$\triangle \color{red}{XY}Z $$
- LJ of $$ \triangle \color{red}{J}K\color{red}{L} $$ corresponds with side ZX of$$\triangle \color{red}{X}Y \color{red}{Z}$$
Below is a picture of what these two triangles could look like
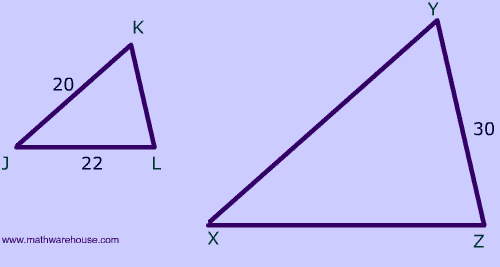
Practice Problems
Pick a pair of corresponding sides (follow the letters)
AB and AD are corresponding based on the letters of the triangle names
$$ \triangle \color{red}{AB}C $$ ~ $$ \triangle \color{red}{AD}E $$
Substitute side lengths into proportion
$$ \frac{AB}{AD} = \frac{20}{30} $$
Simplify (if necessary)
$$ \frac{20}{30} = \frac{2}{3} $$
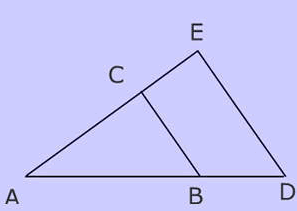
Part B) If EA = 33, how long is CA?
EA and CA are corresponding sides ( $$ \triangle \color{red}{A}B\color{red}{C}$$ ~ $$\triangle \color{red}{A}D\color{red}{E}$$ )
Since the sides of similar triangles are proportional, just set up a proportion involving these two sides and the similarity ratio and solve.
$ \frac{EA}{CA} = \frac{3}{2} \\ \frac{33}{CA} = \frac{3}{2} \\ CA \cdot 3 = 2 \cdot 33 \\ CA \cdot 3 = 66 \\ CA = \frac{66}{3} = 22 $
DE = 27, how long is BC?
EA and AC are corresponding sides ($$ \triangle \color{red}{ A}B\color{red}{C}$$ ~ $$\triangle \color{red}{A}D\color{red}{E}$$)
Since the sides of similar triangles are proportional, just set up a proportion involving these two sides and the similarity ratio and solve.
$ \frac{DE}{BC} = \frac{3}{2} \\ \frac{27}{CA} = \frac{3}{2} \\ CA \cdot 3 = 2 \cdot 27 \\ CA \cdot 3 = 54 \\ CA = \frac{54}{3} = 18 $
Problem 2
Use your knowledge of similar triangles to find the side lengths below.
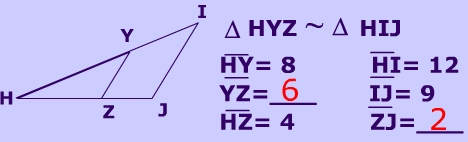
Pick a pair of corresponding sides (follow the letters)
HY and HI are corresponding sides
$$ \triangle \color{red}{HY}Z$$ ~ $$\triangle \color{red}{HI}Y$$
Substitute side lengths into proportion
$$\frac{HY}{HI } = \frac{8}{12}$$
(You could, of course, have flipped this fraction if you wanted to put HI in the numerator $$\frac{HI}{HY}$$ )Simplify (if necessary)
$$ \frac{8}{12}=\frac{2}{3} $$
Set up equation involving ratio and a pair of corresponding sides
$$ \frac{2}{3} =\frac{YZ}{IJ} \\ \frac{2}{3} =\frac{YZ}{9} \\ \frac{2 \cdot 9}{3} =YZ \\ YZ = 6 $$
Finding ZJ is a bit more tricky . You could use the side splitter short cut . Or you use the steps up above to find the length of HJ ,which is 6 and then subtract HZ (or 4) from that to get the answer.
