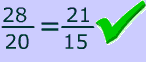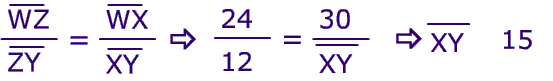Mathwarehouse Logo

Triangle Angle Bisector Theorem

What is the Angle Bisector theorem?

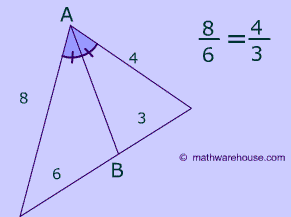
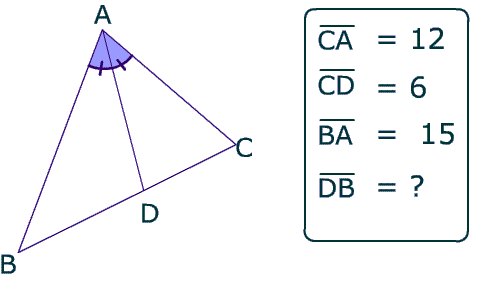
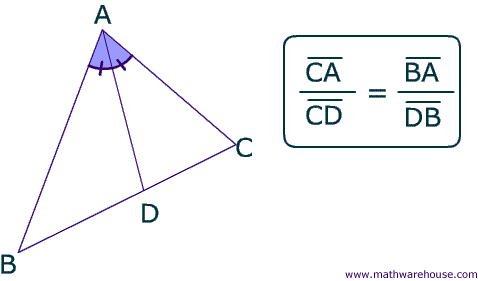
Answer: As you can see in the picture below, the angle bisector theorem states that the angle bisector, like segment AD in the picture below, divides the sides of the a triangle proportionally.

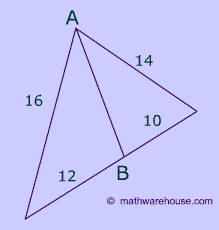
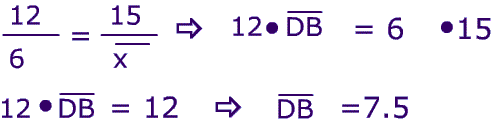
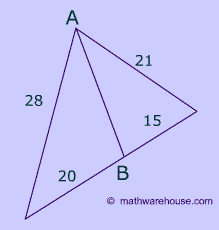
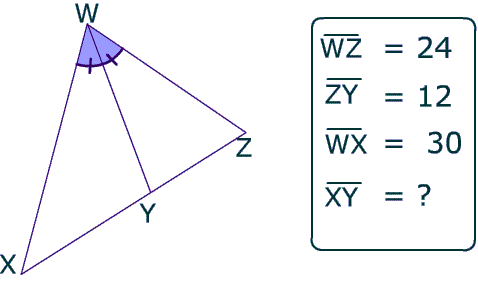
Picture of Angle Bisector Theorem Example

The picture below shows the proportion in action.

picture of angle bisector theorem formula

Is side AB an angle Bisector?

Look at the measurements of the side lengths below to help you decide.

angle bisector
Hint, please

AB is an angle bisector if it divides the triangle proportionally.

AB is not an angle bisector because it does not create two proportional triangles.

$ \frac{14}{10} \color{Red}{ \ne} \frac{16}{12} $

How about side AB below? Is it an angle bisector?

angle bisector
Hint, please

AB is an angle bisector if it divides the triangle proportionally.

Yes, AB is n angle bisector because it divides the triangle proportionally.

equal

Interactive Demonstration

$$ \frac{CA}{CD} = \frac{BA}{BD} \\ \frac{\class{side-ca}{3.86}}{\class{side-cd}{3.86}} = \frac{\class{side-ba}{2.35}}{\class{side-bd}{2.35}} \\ \class{side-final}{1} = \class{side-final}{1} \\ $$
Drag Circles to Start Demonstration

Practice Problems

Problem 2

What is the length of XY in the triangle below?

Angle bisector theorem problem
angle bisector
Back to Similar Triangles

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!