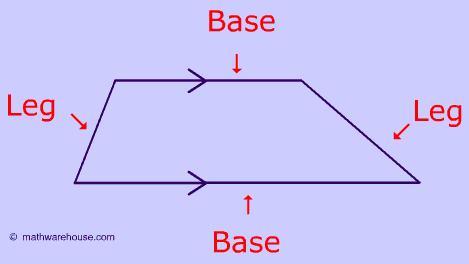
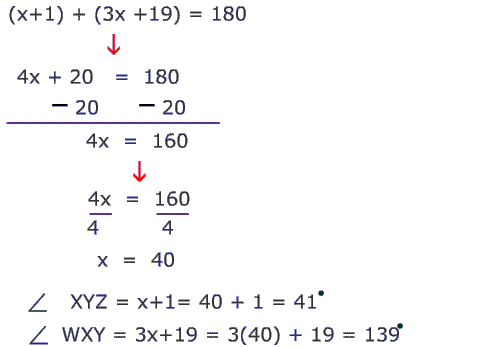A trapezoid is a quadrilateral with one pair of parallel lines
Bases - The two parallel lines are called the bases.
The Legs - The two non parallel lines are the legs.
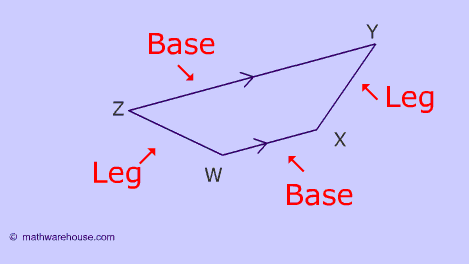
A trapezoid is a quadrilateral with one pair of parallel lines
Bases - The two parallel lines are called the bases.
The Legs - The two non parallel lines are the legs.
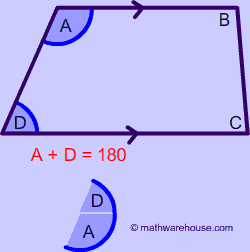
The angles on the same side of a leg are called adjacent angles such as $$\angle A $$ and $$ \angle D $$ are supplementary. For the same reason, $$ \angle B $$ and $$ \angle C $$ are supplementary.
$$ \angle ZWX = 180 − 44 = 136° $$
$$ \angle MLO = 180-124 = 56° $$
If LMNO is a trapezoid and its bases LO and MN are parallel then, $$ \angle MNO $$ and $$ \angle NOL $$ which must be supplementary however, the sum of these angles is not 180 111 + 68 ≠ 180.
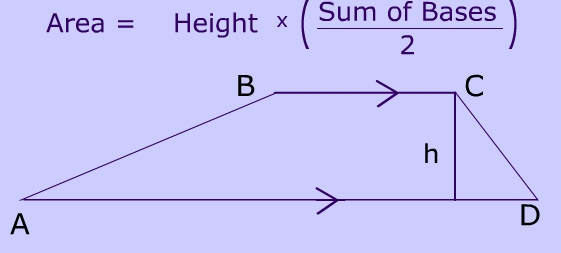
$ Area = height \cdot \left( \frac{ \text{sum bases} }{ 2 } \right) \\ = 7 \cdot \left( \frac{ 4 + 8 }{ 2 } \right) \\ =7 \cdot \left( \frac{ 12 }{ 2 } \right) \\ = 7 \cdot 6 \\ = \fbox {42 } ft^2 $
The midsegment of a trapezoid is:
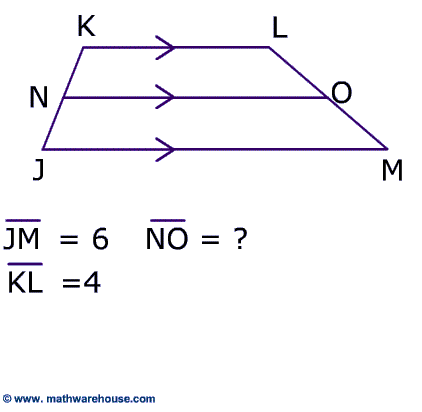
To calculate the length of the midsegment find the average of the bases length of midsegment = (6 + 4) / 2 = 5.
The midpoint of the red segment pictured below is the point $$(A, 2b)$$ (click button below to see).
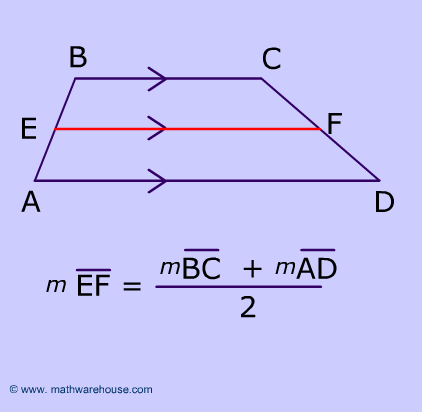
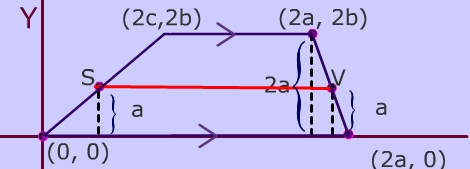
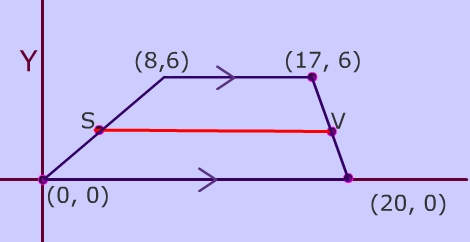
The midsegment of a trapezoid is the segment that joins the midpoints of the nonparallel sides of a trapezoid.
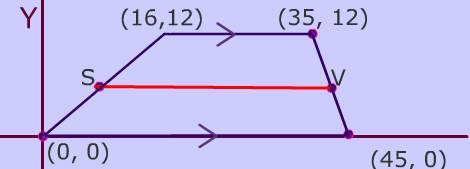
In the trapezoid below, the midpoints of the non-parallel sides are points S and V. The midsegment is the red line segment from S to V.
It is not a true midsegment because its length does