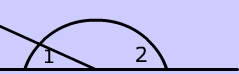
Supplementary Angles

Supplementary angles are a ngles whose sum is 180 °

No matter how large or small angles 1 and 2 on the left become, the two angles remain supplementary which means that they add up to 180°.

By the way, supplementary angles do not need to be adjacent angles(angles next to one another)

Interactive Supplementary Angles

Click and drag around the points below to explore and discover the rule for vertical angles on your own. You can click and drag points A, B, and C.

(Full Size Interactive Supplementary Angles)

Practice Problems

1 =32 °
What is m

Angle 2

fraction games onlinemathgames.comlaw of sinesambiguous case of the law of sines