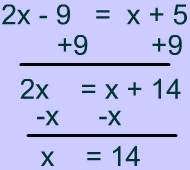A rhombus is a type of parallelogram, and what distinguishes its shape is that all four of its sides are congruent.
There are several formulas for the rhombus that have to do with its:
Probably the most famous rhombus out there is the baseball diamond. The distance between each base is the same, making the shape a rhombus!
More interesting math facts!
Is a Square a Rhombus?
Answer:Yes, a square is a rhombus
A square must have 4 congruent sides. Every rhombus has 4 congruent sides so every single square is also a rhombus. A square is a special rhombus that also has 4 right angles.
Keep in mind that the question "Is a square a rhombus?" means Is every square also always a rhombus?
Is Rhombus a Square?
Answer:No, a rhombus is not a square
A square must have 4 right angles. A rhombus, on the other hand, does not have any rules about its angles, so there are many many, examples of a rhombus that are not also squares.
Keep in mind that the question "Is a rhombus a square?" means Is every rhombus also always a square?
Diagram 2
![]()
As you can see in diagram 2, it is possible to create a rhombus that is not a square .
Sides
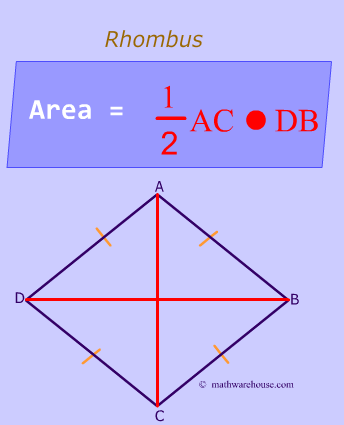
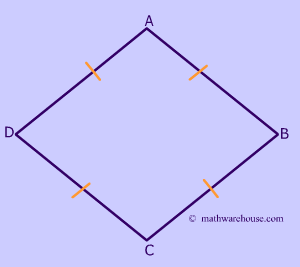
All sides of a Rhombus are congruent.
$
\overline{AB} \cong \overline{BC}
\\
\overline{BC} \cong \overline{CD}
\\
\overline{CD} \cong \overline{DA}
$
Angles
Diagonals
Diagonals are perpendicular.
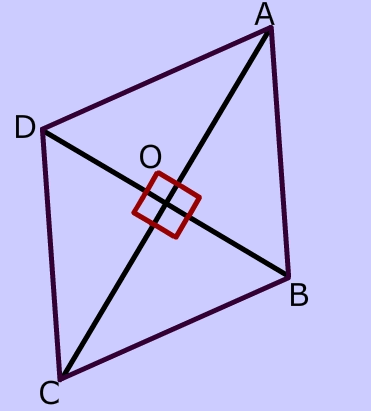
$$ \angle AOD = 90^{\circ} \\ \angle AOB = 90^{\circ} \\ \angle BOC = 90^{\circ} \\ \angle COD = 90^{\circ} \\ $$
Area of Rhombus
Alex please put the rhombus calculator here
input
1) side length
2) output -- angle measurements and area
Practice Problems
Putting It All Together
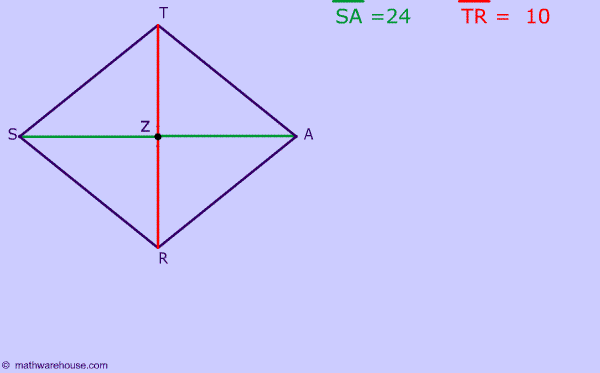
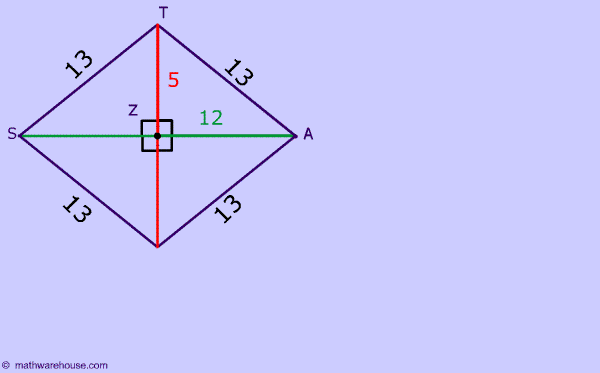
STAR is a rhombus. The measure of diagonals SA is 24 and the measure of TR is 10, what is the perimeter of this rhombus?
Ask yourself: What is true about the angles formed by the diagonals of a rhombus?
What kind of triangle is
ZTA?
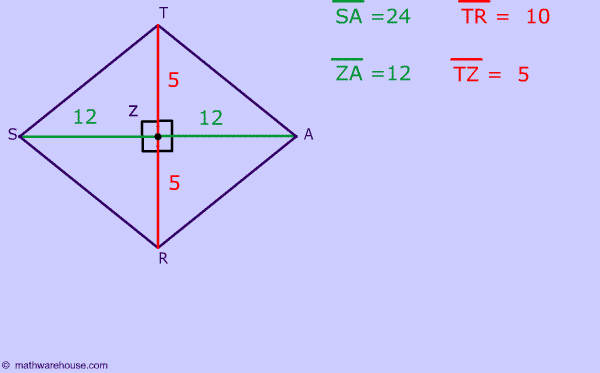
Now, that you know the length of TA? How can you use the fact that the sides of a rhombus are congruent to finish this problem?
Since, all 4 sides must be 13.
The perimeter = 13 + 13 + 13 +13 = 52
Problem 1
If side WX = 22, what is WZ?
WZ = 22
Problem 2
If side MN of rhombus LMNO is X + 5 and side LM is 2x − 9, what must be the value of x?
Problem 3
What must be the value of x, if side BA = 5x-11
and side
AD = 6x-18?
Since this shape is a rhombus you can set any of its sides equal to each other.
Problem 4
Is the four-sided shape below, MNOP, a rhombus? If not, classify the shape.
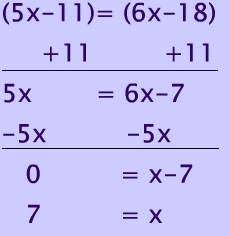
The shape below is not a rhombus because its diagonals are not perpendicular.
However, since opposite sides are congruent and parallel, and the diagonals bisect each other. The shape below is a parallelogram.
Problem 5
What is the measure of the following angles in rhombus ABCD?
ACD
= 46°
ABD
= 44°
Problem 6
A generalization about the angles of a rhombus
You can think of a rhombus as four triangles that are created by the diagonals such as
What is true about the outside angles in each triangle? An examples of outside angles are
Since the diagonals of a rhombus are perpendicular, these outside angles must be complementary angles.
Problem 7
What is the value of x if
BCA = 3x -2
and
ACD = 12 + x
?
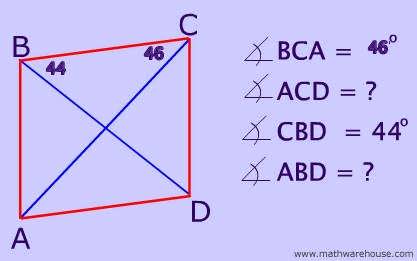
Since diagonals bisect vertex angles,
BCA
ACD
Problem 8
What is the value of x, given the angle measurements below?
Problem 9
What is the area of HIJK?
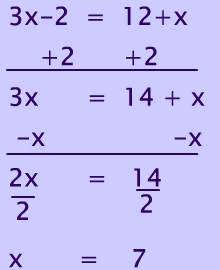
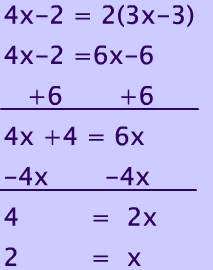
Area = ½(IK × HJ) = ½ (9 × 12) = 54
Properties of Rhombus:
Related:
