What is a remainder?
The amount left over when you divide two numbers.
For instance, let's examine $$ 11 \div 2 $$.
When you divide 11 by 2, you end up with 1 'left over' as shown in the worked out long division below:
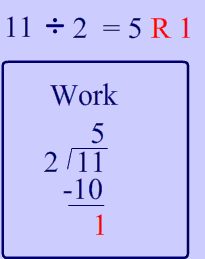
Learn how to work with remainders with our examples and pictures.
The amount left over when you divide two numbers.
For instance, let's examine $$ 11 \div 2 $$.
When you divide 11 by 2, you end up with 1 'left over' as shown in the worked out long division below:
Let's examine $$ 7 \div 2$$.
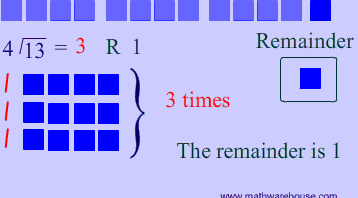
Let's examine $$ 11 \div 4$$.
Let's examine $$ 11 \div 3$$.
Let's examine $$ 14 \div 5$$.
Find the remainder for each problem below.
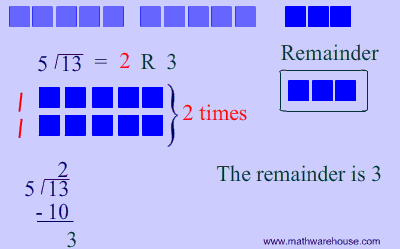
As you can see in the picture below, the remainder is 3.
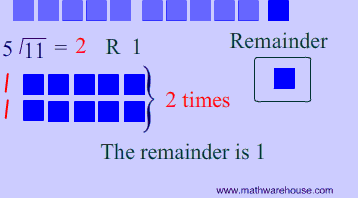
As you can see in the picture below, the remainder is 1.
As you can see in the picture below, the remainder is 0.
When a number (like 5 up above) evenly divides the other (10 above), then there is no remainder.
As you can see in the picture below, the remainder is one.
![]() The problems below are "next-level". See how you do!
The problems below are "next-level". See how you do!
The answer to this problem is easier to understand if you look at the long division work.
The answer to this problem is easier to understand if you look at the long division calculations. Three goes into zero, zero times and when you do the long division you'll actually see that there is not any remainder.
The answer to this problem is easier to understand if you look at the long division work.
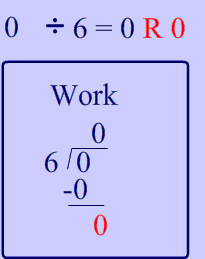
The answer to this problem is easier to understand if you look at the long division calculations. 6 goes into zero, zero times and when you do the long division you'll actually see that there is not any remainder.
Yes, you actually can indeed answer this question because zero divided by any number is zero and has a remainder of zero!