Quick Overview
Suppose $$\red n\neq 0$$. Then...
- If $$\displaystyle\lim\limits_{x\to a} f(x) = \frac{ \red n}{0} $$, the limit does not exist.
- The $$\frac {\red n}{0}$$ form tells us the function is becoming infinitely large.
- If the one-sided limits are the same, we say
$$\displaystyle\lim\limits_{x\to a} f(x) = \infty\qquad\mbox{or}\qquad\lim\limits_{x\to a} f(x) = -\infty$$.
Notation
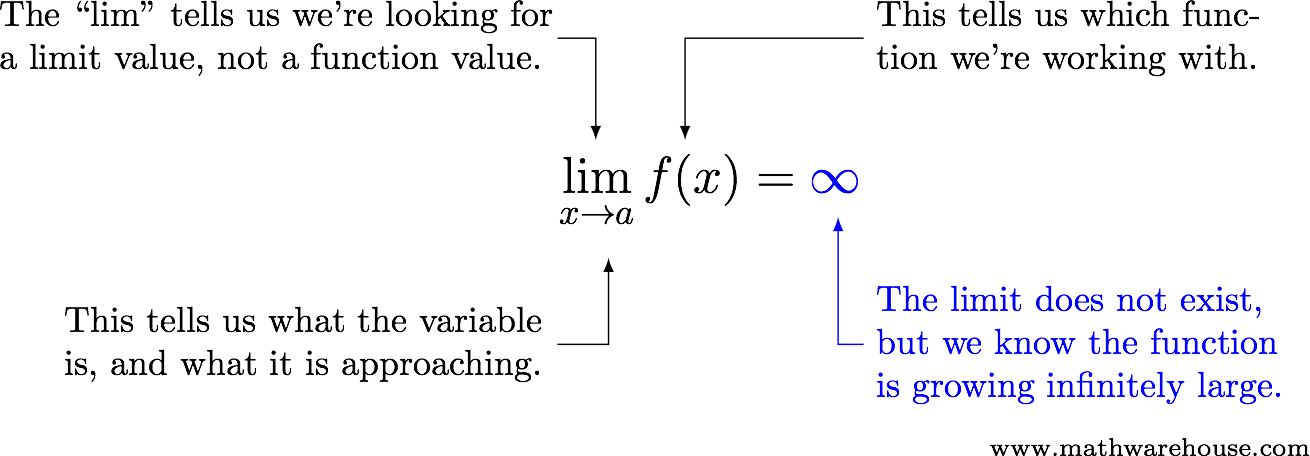
Examples
Example 1
Evaluate $$\displaystyle \lim_{x\to0}\,\frac 1 {x^2}$$
Determine the form of the limit.
$$ \lim_{x\to0}\,\frac 1 {x^2} % = \frac{\red 1}{0} \qquad \left(\frac{\red n}{0} \mbox{ form}\right) $$
Since the limit has the $$\frac{\red n}{0}$$ form, we know the limit does not exist. However, it still might be an infinite limit.
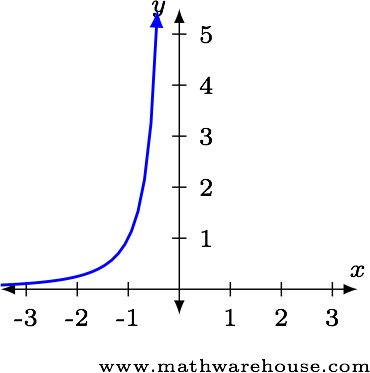
Examine the left-hand limit.
- The numerator is positive.
- Since the denominator is $$x^2$$, it will be positive.
- The $$\frac{\red n}{0}$$ form tells us the function is becoming infinitely large.
Taken together, these three statements tell us $$\displaystyle \lim_{x\to0^-}\,\frac 1 {x^2} = \infty$$
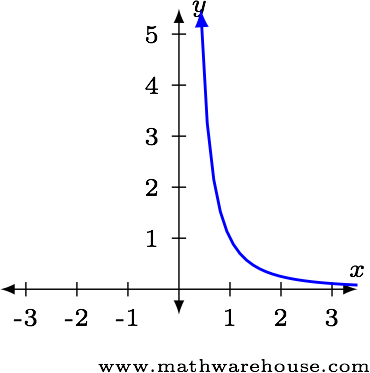
Examine the right-hand limit.
- The numerator is positive.
- Since the denominator is $$x^2$$, it will be positive.
- The $$\frac{\red n}{0}$$ form tells us the function is becoming infinitely large.
Taken together, these three statements tell us $$\displaystyle \lim_{x\to0^+}\,\frac 1 {x^2} = \infty$$
Conclusion
Both one-sided limits tell us the function is growing infinitely large in the positive direction. Since the one-sided limits indicate the same behavior, the limit is infinite.
Answer: $$\displaystyle \lim_{x\to0}\,\frac 1 {x^2} = \infty$$
Example 2
Evaluate: $$\displaystyle \lim_{x\to 3}\,\frac 1 {x-3}$$
Determine the form of the limit.
$$\displaystyle\lim_{x\to 3}\,\frac 1 {x-3} = \frac 1 {3-3} = \frac{\red 1}{0}$$
The limit does not exist since it has the $$\frac{\red n}{0}$$ form. It might also be an infinite limit.
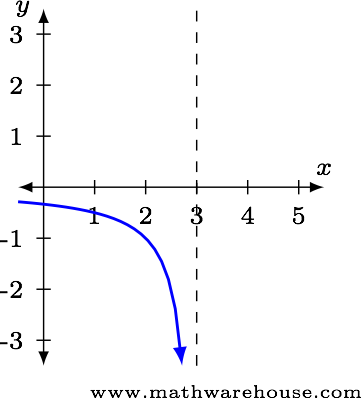
Examine the left-hand limit.
- The numerator is always positive.
- The denominator will be negative, since $$x<3$$.
- The function is becoming infinitely large.
Taken together, these statements tell us $$\displaystyle \lim_{x\to 3^-}\,\frac 1 {x-3} = -\infty$$
Examine the right-hand limit.
- The numerator is always positive.
- The denominator will be positive, since $$x>3$$.
- The function is becoming infinitely large.
Taken together, these statements tell us $$\displaystyle \lim_{x\to 3^+}\,\frac 1 {x-3} = \infty$$

Conclusion
Since the one-sided limits are different, the limit does not exist.
Answer: $$\displaystyle \lim_{x\to 3}\,\frac 1 {x-3}$$ does not exist.
Example 3
Evaluate: $$\displaystyle \lim_{x\to2}\,\frac{x-5}{x^2-4x+4}$$
Determine the form of the limit.
$$ \displaystyle\lim_{x\to2}\,\frac{x-5}{x^2-4x+4} % = \frac{2-5}{(2)^2-4(2)+4} % = \frac{-3}{(2)^2-4(2)+4} % = \frac{\red { -3}}{0} $$
The limit does not exist, but it might be an infinite limit.
Factor the denominator to make our analysis easier.
$$ \displaystyle\lim_{x\to2}\,\frac{x-5}{x^2-4x+4} % = \displaystyle\lim_{x\to2}\,\frac{x-5}{(x-2)^2} $$
Examine the one-sided limits.
- For both limits, the numerator will be -3.
- Since the denominator is being squared, it will always be positive.
- The function becomes infinitely large as $$x$$ approaches 2.
Since the numerator and denominator have opposite signs, the function will grow infinitely large in the negative direction.
Answer: $$\displaystyle \lim_{x\to2}\,\frac{x-5}{x^2-4x+4} = -\infty$$














