Quick Overview
- "Limits at Infinity" examine what happens to the function value as $$x$$ becomes infinitely large.
- For a limit at infinity to exist, the function has to approach a particular, finite value.
- Horizontal asymptotes are defined as limits at infinity.
Horizontal Asymptotes
Recall that an asymptote is a value that the function becomes really, really close to as $$x$$ becomes larger and larger, like in the graph below.

This is exactly the idea of a limit at infinity!
Definition
Suppose $$f(x)$$ becomes arbitrarily close to a particular finite value $$L$$ as $$x$$ becomes infinitely large. Then $$L$$ is the limit of $$f(x)$$ as $$x$$ goes to infinity, and we write
$$ \displaystyle\lim_{x\to\infty} f(x) = L. $$
Notation Explanation
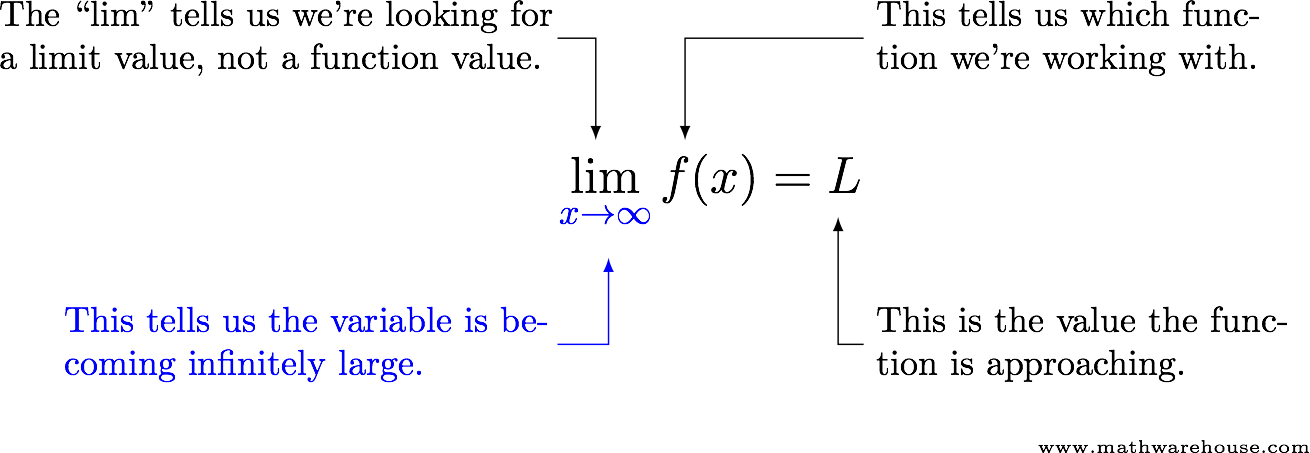
Limits at Negative Infinity
Similarly, $$\displaystyle \lim_{x\to-\infty} f(x) = L$$ means the function approaches $$L$$ as $$x$$ grows infinitely large in the negative direction.
Estimating Limits at Infinity with Graphs and Tables
Example 1
Use the graph below to estimate $$\lim\limits_{x\to\infty} f(x)$$.
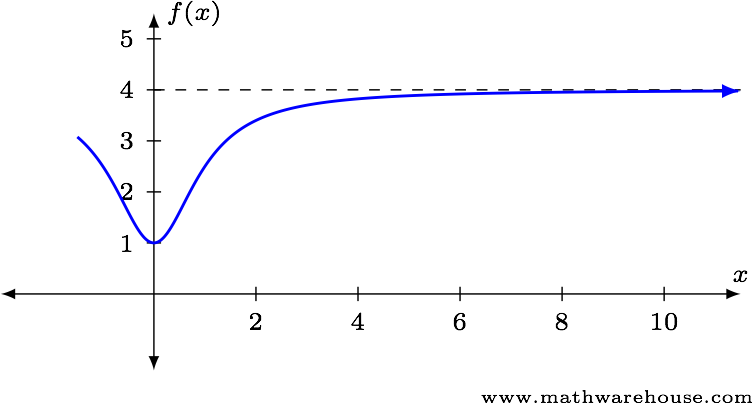
The graph seems to indicate the function value gets close to 4 as $$x$$ grows larger.
Answer$$ \lim\limits_{x\to\infty} f(x) \approx 4 $$
Example 2
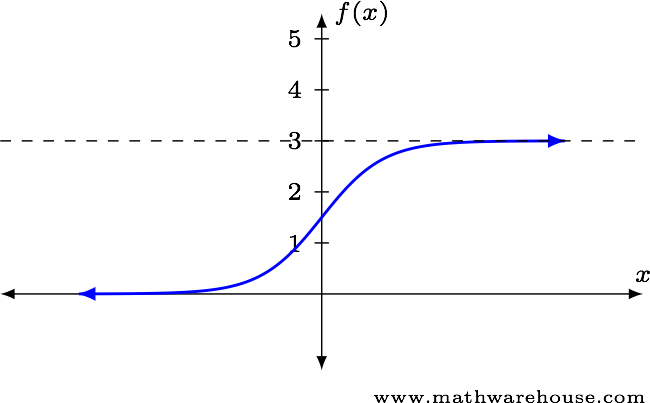
Use the graph below to estimate the value of
- $$\displaystyle \lim_{x\to\infty} f(x)$$
- $$\displaystyle \lim_{x\to-\infty} f(x)$$
 Answer
Answer
- $$\displaystyle \lim_{x\to\infty} f(x) \approx 3$$
- $$\displaystyle \lim_{x\to-\infty} f(x) \approx 0$$
Example 3
Use the table below to estimate $$\lim\limits_{x\to-\infty} f(x)$$.
$$ \begin{array}{c|c} {x} & {f(x)}\\ \hline -10 & 8.5\\ -50 & 8.1\\ -100 & 8.013\\ -1000 & 8.0014\\ -10000 & 8.00013\\ -100000 & 8.000014 \end{array} $$
The larger $$x$$ gets in the negative direction, the closer the function seems to get to 8.
Answer$$ \lim\limits_{x\to-\infty} f(x) \approx 8 $$
When Limits at Infinity Don't Exist
In order for a limit at infinity to exist, the function must approach a particular finite value. Consider the following example.
Example 4
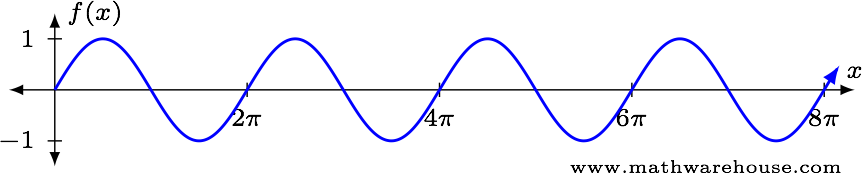
Examine $$\lim\limits_{x\to\infty} \sin x$$.
SolutionThe sine function always oscillates between 1 and $$-1$$. No matter how large the $$x$$-value becomes, this behavior won't change (see below).
 Answer
Answer
$$\lim\limits_{x\to\infty} \sin x$$ does not exist.
Infinite Limits at Infinity
If the function value becomes infinitely large as $$x$$ grows larger, we can use the idea of infinite limits to describe what is happening to the function.
Example 5
Examine $$\lim\limits_{x\to\infty} x^2$$.
SolutionAs $$x$$ grows larger, $$x^2$$ will too.
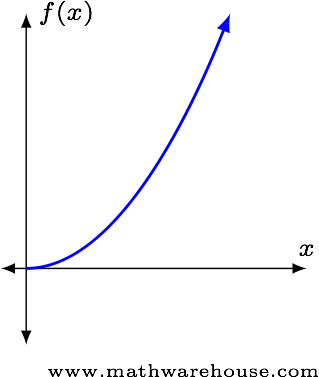
Since $$x^2$$ will eventually become larger than any particular value, we can say the function becomes infinitely large.
Answer$$ \displaystyle \lim_{x\to\infty} x^2 = \infty $$
Important! Just as before, saying the limit is infinite also means the limit does not exist.
Example 6
Use the graph of $$f(x) = x + \frac 1 3 x\sin 2x$$ to understand $$\displaystyle\lim_{x\to\infty} f(x)$$.
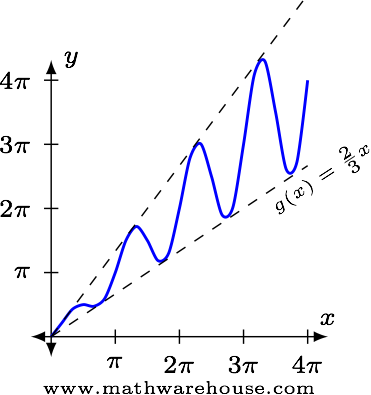
Even though the function oscillates, it never falls beneath the line $$g(x) = \frac 2 3 x$$. One of the limit laws tells us that since $$f(x) \geq g(x)$$, then $$\lim\limits_{x\to\infty} f(x) \geq \lim\limits_{x\to\infty} g(x) = \infty$$.
Answer$$ \lim\limits_{x\to\infty} f(x) = \infty $$
Example 7
Use the graph below to understand $$\displaystyle \lim_{x\to\infty} x\sin^2(2x)$$.
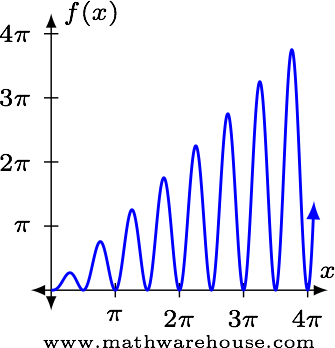
The oscillations of this function continue to increase in amplitude, but since the function always returns to the $$x$$-axis, we can't say the limit is infinite.
Answer$$\lim\limits_{x\to\infty} x\sin^2(2x)$$ does not exist.


















