Students are often asked to find the equation of a line that is parallel to another line and that passes through a point. Watch the video tutorial below to understand how to do these problems and, if you want, download this free worksheet if you want some extra practice.
Video Tutorial
Example
Method 1: Using Slope Intercept Form
What is the equation of line parallel to $$ y = 3x + 5 $$ and through the point $$ (1, 7) $$?
Many students are more comfortable using slope intercept form but this kind of problem is actually much easier, using point slope form (shown immediately below)
Step 1
Substitute the slope from original line (3 in this case) into the equation of the line
Step 2
$ y = \red 3 x + b $
Substitute the given point (1, 7) into the x and y values
Step 3
$ y = \red 3 x + b \\ 7 = \red 3 (1) + b $
Solve for b (the y-intercept)
$ \begin{align*} 7 &= 3 (1) + b \\ 7 &= 3 + b \\ -3 & -3 \\ \hline \\ 4 &= b \\ \end{align*} $
Step 4Substitute this value for 'b' in the slope intercept form equation $ y = 3x + 4 $
Method 2: Using Post Slope Form
What is the equation of line parallel to y = 3x + 5 and through the point (1, 7)?
If you're comfortable with point slope form, this is the way to go! Just look how little work there is to do! In fact, all that you have to do is substitute twice!
Step 1
Substitute the slope from original line (3 in this case) into the point slope equation
y - y1 = m(x - x1)
y - y1 = 3(x - x1)
Substitute the given point (1, 7) into the x1 and y1 values y - 7= 3(x - 1)
Practice Problems
Problem 1 - Method 1
Step 1
Substitute slope from original line (4 in this case) into the slope intercept equation.
$ y = \red 4 x + b $
Step 2
Substitute the given point $$(5, 9) $$ into the x and y values.
$
y = 4x + b
\\
9 = 4(5) + b
$
Step 3
Solve for b (the y-intercept).
$ \begin{align*} 9 &= 4 (5) + b \\ 9 &= 20 + b \\ -20 & -20 \\ \hline \\ -11 &= b \\ \end{align*} $
Step 4
Substitute this value for 'b' in the slope intercept form equation.
$$ y = 4x - 11 $$
Problem 1 - Method 2
Step 1
Substitute the slope from original line (4 in this case) into the point slope equation.
y - y1 = m(x - x1)
y - y1 = 4(x - x1)
Step 2
Substitute the given point (5, 9) into the x1 and y1 values.
y - 5 = 4(x - 9)
Problem 2 - Method 1
Step 1
Substitute slope from original line (¾ in this case) into the slope intercept equation.
y = ¾x + 22
Step 2
Substitute the given point (-8, 11) into the x and y values.
y = ¾x + b
11 = ¾(-2) + b
Step 3
Solve for b (the y-intercept).
Step 4
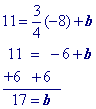
Substitute this value for 'b' in the slope intercept form equation.
y = ¾x + 17
Problem 2 - Method 2
Step 1
Substitute the slope from original line (¾ in this case) into the point slope equation.
y - y1 = m(x - x1)
y - y1 = ¾(x - x1)
Step 2
Substitute the given point (-8, 11) into the x1 and y1 values.
y - 11= ¾(x + 8)
Problem 3 - Method 1
Step 1
Substitute slope from original line (-¼ in this case) into the slope intercept equation.
y = -¼x + 22
Step 2
Substitute the given point (32, -4) into the x and y values.
y = -¼x + b
-4 = -¼(32) + b
Step 3
![work]()
Solve for b (the y-intercept).
Step 4
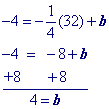
Substitute this value for 'b' in the slope intercept form equation.
y = -¼x + 4
Problem 3 - Method 2
Step 1
Substitute the slope from original line (-¼ in this case) into the point slope equation.
y - y 1 = m(x - x1)
y - y1 = - ¼(x - x1)
Step 2
Substitute the given point (32, -4) into the x1 and y1 values.
y + 4 = - ¼(x - 32)
