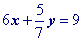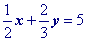It is a common task to have to convert the equation of a line from standard form to point slope form.

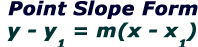
Video Tutorial on Standard to Point Slope Form
Example Problem
Isolate the $$\red y$$ term.
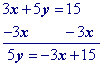
Multiply all terms by the multiplicative inverse of the coefficient of y.
Simplify.
Substitute a convenient value for x into your equation and then solve for y.
You're doing this to get the values of $$ ( \blue{x_1}, \blue{y_1}) $$ for the point slope formula : $$ y - \blue y_1 = m(x - \blue x_1) $$
Remember that you can pick any value that you want. You're just choosing a value for $$x$$ and then finding its associated $$y $$ value.
Let's choose $$x = \blue 5$$. Yes, you could choose x = 0 and make your life really easy! After you solve for the y value, then .
$$ y = - \frac 3 5 x + 3 \\ \text{ Let's choose } x = \blue 5 \\ y = -\frac 3 5 \cdot \blue 5 + 3 \\ y = -3 + 3 \\ y = \blue 0 \\ \text{ Or, using } x = \blue 0 \\ y = - \frac 3 5 x + 3 \\ y = -\frac 3 5 \cdot \blue 0 + 3 \\ y = \blue 3 $$Substitute the x value you picked and y value you solved for into the general form of point slope formula.
Note that both of the above equations are equivalent. They both are valid. Neither equation is 'better'.
Practice Converting Equations
Isolate the $$\red y $$ term.
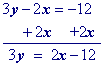
Multiply all terms by the multiplicative inverse of the coefficient of y.
Simplify.
Substitute a convenient value for x into your equation and then solve for y.
You're doing this to get the values of $$ ( \blue{x_1}, \blue{y_1}) $$ for the point slope formula : $$ y - \blue y_1 = m(x - \blue x_1) $$
Remember that you can pick any value that you want. You're just choosing a value for $$x$$ and then finding its associated $$y $$ value.
Let's choose $$x = \blue 3$$. Yes, you could choose x = 0 and make your life really easy! After you solve for the y value, then .
$$ y = \frac 2 3 x - 4 \\ \text{ Using } x = \blue 3 \\ y = \frac 2 3 \cdot \blue 3 - 4 \\ y = 2 -4 \\ y = - 2 \\ \text{ Or, using } x = \blue 0 \\ y = \frac 2 3 \cdot \blue 0 - 4 \\ y = -4 $$Substitute the x value you picked and y value you solved for into the general form of point slope formula.
Note that both of the above equations are equivalent. They both are valid. Neither equation is 'better'.
Isolate the $$\red y$$ term.
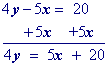
Multiply all terms by the multiplicative inverse of the coefficient of y.
Simplify.
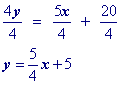
Substitute a convenient value of x into your equation and solve for y (You're doing this to get the point x1, y1). Let's choose x = 3. Yes, you could choose x = 0 and make your life really easy!Then substitute the x and y values that found into the point slope formula.
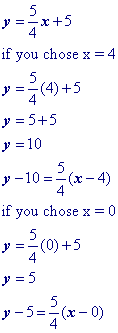
Isolate the 'y' term.
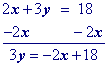
Multiply all terms by the multiplicative inverse of the coefficient of y.
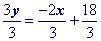
Simplify.
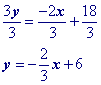
Substitute a convenient value of x into your equation and solve for y (You're doing this to get the point x1, y1). Let's choose x = 3. Yes, you could choose x = 0 and make your life really easy!Then substitute the x and y values that found into the point slope formula.
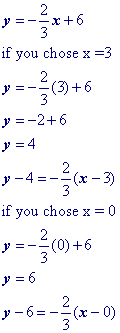
More challenging problems
Isolate the 'y' term.
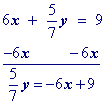
Multiply all terms by the multiplicative inverse of the coefficient of y.
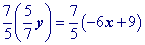
Simplify.
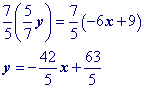
Substitute a convenient value of x into your equation and solve for y (You're doing this to get the point x1, y1). Let's choose x = 3. Yes, you could choose x = 0 and make your life really easy!Then substitute the x and y values that found into the point slope formula.
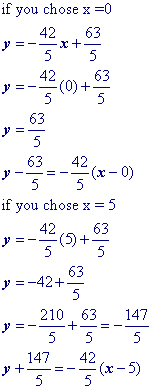
Isolate the 'y' term.
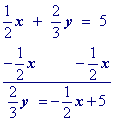
Multiply all terms by the multiplicative inverse of the coefficient of y.
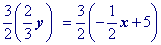
Simplify.
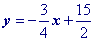
Substitute a convenient value of x into your equation and solve for y (You're doing this to get the point x1, y1). Let's choose x = 3. Yes, you could choose x = 0 and make your life really easy!Then substitute the x and y values that found into the point slope formula.
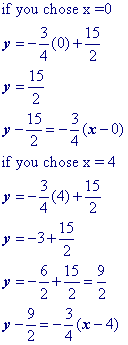
- Linear Equations
- Equation of Line Formula
- Slope Intercept Form
- Standard Form of Line
- Point Slope to Standard Form
- Linear Equations Worksheets (standard form, slope intercept form and more)