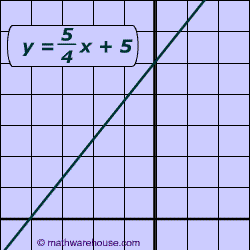
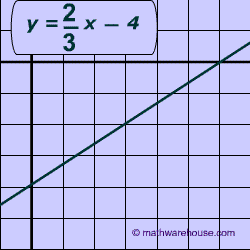
It is a common to ask to have to convert equation of line from slope intercept to standard form, as demonstrated by the pictures below.

Example of Converting from Slope Intercept to Standard Form
Multiply by the least common denominator of the fractions (if any)
The only fraction is $$ \frac { 5}{ \red 4} $$ so you can multiply everything by 4.
$ \red 4 \cdot y = \red 4 \cdot \big( \frac { 5}{ \red 4}x +5 \big)
\\ 4y = 5x + 20
$
Move" y1 to the other side by adding its opposite to both sides of the equation and simplify
Solve for the y-intercept (or "b" in the slope intercept equation) which is 20 in this example.
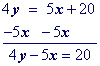
Use our Calculator
You can use the calculator below to find the equation of a line from any two points. Just type numbers into the boxes below and the calculator (which has its own page here) will automatically calculate the equation of line in standard and slope intercept forms

Answer:
$ $
( Try this 'equation from 2 points' calculator on its own page here . )
Practice Problems
Multiply by the least common denominator of the fractions
The only fraction is $$ \frac{2}{\red 3 } $$ so you can multiply everything by 3.
$$ \red 3 \cdot y = \red 3 \big( \frac{2}{\red 3 } -4 \big) \\ 3y = 2x-12 $$
Solve for the y-intercept (or "b" in the slope intercept equation) which is 12 in this problem.
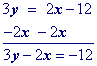
Multiply by the least common denominator of the fractions (if any)
The only fraction is $$ \frac{1}{\red 2}$$ so you can multiply everything by 2.
$$ \red 2 \cdot y =\red 2 \cdot \big( \frac{1}{\red 2} x + 5 \big) \\2y = x + 10 $$
Solve for the y-intercept (or "b" in the slope intercept equation) which is 10 in this problem.
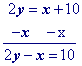
Multiply all terms by the least common denominator of the fractions
Unlike the prior examples, this problem has two fractions $$ \big( \frac 2 3 \text{ and } \frac 5 9 \big) $$ so you can multiply everything by their common denominator of $$ \red 9$$ .
$$ \red 9 \cdot y = \red 9 \big( \frac 2 3 x + \frac 5 9 \big) \\ 9y = 6x + 5 $$
Solve for the y-intercept (or "b" in the slope intercept equation) which, in this example, is 5.
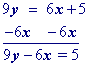
Multiply all terms by the least common denominator of the fractions
This problem only has the fraction $$ \frac{4}{\red 7 } $$ so we must multiply everything by 7.
$$ \red 7 \cdot y = \red 7 \big( 5x + \frac 4 7 \big) \\ 7y = 35x + 4 $$
Solve for the y-intercept (or "b" in the slope intercept equation) which, in this example, is 4.
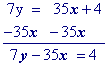
Multiply all terms by the least common denominator of the fractions
This problem only has the fraction $$ \frac{b}{ \red c } $$ so we must multiply everything by $$ \red c $$.
$$ \red c \cdot y = \red c \big( ax + \frac b c \big) \\ cy = cax + b $$ .
Solve for the y-intercept (or "b" in the slope intercept equation) which, in this example, is the variable 'b'.
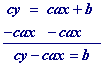
-
Related Links:
- Linear Equations
- Equation of Line Formula
- Slope Intercept Form
- Standard Form of Line
- Standard Form to Slope intercept form
- Linear Equations Worksheets (standard form, slope intercept form and more)