Interactive Parabola Grapher
Explore graph ,equation and the locus of a Parabola
Save graphs to your desktop!



A+    A−    B  
Home
Graphing Calc
Algebra
Math Games
  • Decimals in Space
  • Fraction Balls
  • Integers in Space
  • Math Man
  • Number Balls
    • Geometry
    Interactive
    Trigonometry
    Scientific Calc
    Home
    Graphing Calc
    Algebra
    Math Games
  • Decimals in Space
  • Fraction Balls
  • Integers in Space
  • Math Man
  • Number Balls
    • Geometry
    Interactive
    Trigonometry
    Scientific Calc

    Point Slope Form to Standard Form

    How to convert

    Related Links Equation of Line Formula | Point Slope Form of a Line | Standard Form of Line
    Linear Equations Worksheets (standard form, slope intercept form and more)
    It is a common to ask to have to convert equation of line from point slope form to standard form.
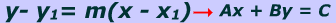
    Video Tutorial on Point Slope to Standard Form
    Example of Converting from Point Slope to Standard Form

    Convert to standard form.
    Step 1) Distribute 'm' or the slope to x −x1 step 1
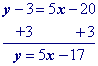
    Step 2)Move" y1 to the other side by adding its opposite to both sides of the equation and simplify step 2
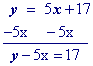
    Step 3) "Move" the x term to the other side by addding its opposite to both sides Step 3


    Practice Converting Equations

    Convert to standard form.
    Step 1) Distribute 'm' or the slope to x −x1 step 1
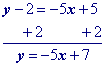
    Step 2) Move" y1 to the other side by adding its opposite to both sides of the equation and simplify step 1
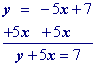
    Step 3) "Move" the x term to the other side by addding its opposite to both sides step 1
    Convert to standard form.
    Step 1) Distribute 'm' or the slope to x −x1 step 1
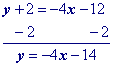
    Step 2) Move" y1 to the other side by adding its opposite to both sides of the equation and simplify step 1
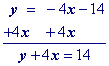
    Step 3) "Move" the x term to the other side by addding its opposite to both sides step 1
    Convert to standard form.
    Step 1) Distribute 'm' or the slope to x −x1 step 1
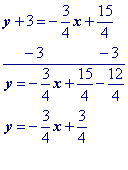
    Step 2)Move" y1 to the other side by adding its opposite to both sides of the equation and simplify step 1
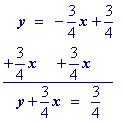
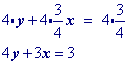
    Step 3) "Move" the x term to the other side by addding its opposite to both sides step 1
    Step 4) An optional step, but if you want integer coefficients, then multiply by the least common multiple of the fractions in the equation step 1
    Convert to standard form.
    Step 1) Distribute 'm' or the slope to x −x1 step 1
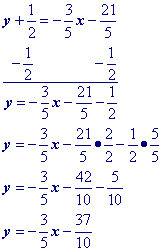
    Step 2) "Move" y1 to the other side by adding its opposite to both sides of the equation and simplify  
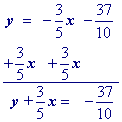
    Step 3) "Move" the x term to the other side by addding its opposite to both sides step 1
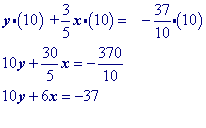
    Step 4) An optional step, but if you want integer coefficients, then multiply by the least common multiple of the fractions in the equation step 1
    Related Links Equation of Line Formula | Point Slope Form of a Line | Standard Form of Line | Standard to Point Slope Form
    Linear Equations Worksheets (standard form, slope intercept form and more)
    site map | copyright & terms of use | Graphing Calculator App | education links| Advanced Online Calculator | Math Homework Answers