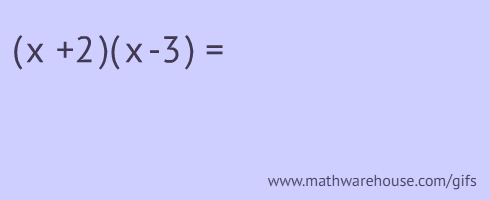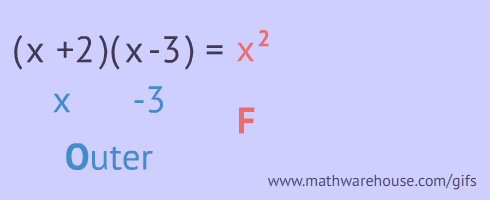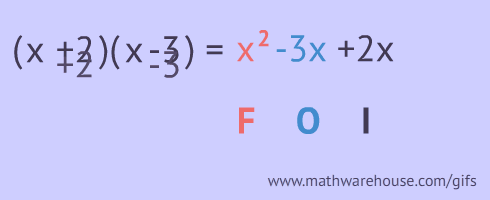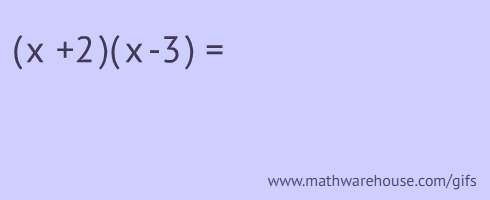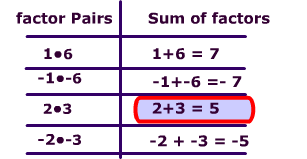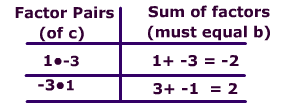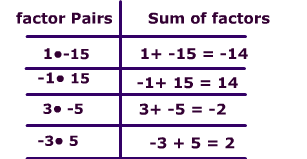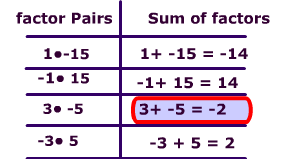How To Factor Trinomials Step By Step tutorial with practice problems. The first step is to..

Formula For Factoring Trinomials (when $$ a = 1 $$ )

It's always easier to understand a new concept by looking at a specific example so you might want scroll down and do that first. This formula only works when $$ a = 1$$ . In other words, we will use this approach whenever the coefficient in front of x² is 1. (If you need help factoring trinomials when $$ a \ne 1 $$, then go here.)

Formula Steps

Identify a, $$ \blue b $$ , and $$\red c $$ in the trinomial $$ ax^2 + \blue bx + \red c $$
Write down all factor pairs of $$\red c $$
Identify which factor pair from the previous step sum up to $$ \blue b $$
Substitute factor pairs into two binomials

Factor $$ x^2 + 5x + 4 $$

Step 1

Identify a, b and c in the trinomial
ax² + bx + c

$$ a = 1 \\ \blue { b = 5} \\ \red { c = 4 } $$

Step 2

Write down all factors of $$ \red c $$ which multiply to $$\red { \fbox {4}} $$

(Note: since $$\red 4 $$ is positive we only need to think about pairs that are either both positive or both negative. Remember a negative times a negative is a positive. As the chart on the right shows you $$-2 \cdot -2 $$ is positive 4 ...so we do have to consider these negative factors.

Step 3

Identify which factor pair from the previous step sums up to $$ \blue b$$

Step 4

Substitute that factor pair into two binomials

$$ (x + 4)(x + 1) $$

Step 5

If you'd like, you can check your work by multiplying the two binomials and verify that you get the original trinomial

$$ (x + 4)(x + 1) = x^2 + 5x + 4 $$

Problem 1

Factor the following trinomial: $$ x^2 + 4x + 3$$

Step 1

Identify a, b and c in the trinomial $$ax^2 + bx + c $$

$$ a = 1 \\ \blue { b =4 } \\ \red{ c = 3} $$

Step 2

Write down all factor pairs of $$ \red 3 $$

(Note: since $$ \red 3 $$ is positive we only need to think about pairs that are either both positive or both negative. Remember a negative times a negative is a positive)

Step 3

Identify which factor pair from the previous step sum up to $$ \blue {4 } $$

Step 4

Substitute that factor pair into two binomials

$$ (x + 3)(x + 1) $$

Step 5

If you'd like, you can check your work by multiplying the two binomials and verify that you get the original trinomial

$$ (x + 3)(x + 1) = x^2 + 4x + 3 $$

Problem 2

Factor the trinomial below $$ x^ 2 + 5x + 6 $$

Step 1

Identify a, b and c in the trinomial ax² + bx + c

$$ a = 1 \\ \blue { b = 5} \\ \red {c = 6} $$

Step 2

Write down all factor pairs of $$ \red 6 $$

Step 3

Identify which factor pair from the previous step sum up to $$ \blue 5$$

Step 4

Substitute that factor pair into two binomials

(x + 2)(x + 3)

Step 5

If you'd like, you can check your work by multiplying the two binomials and verify that you get the original trinomial

(x + 2)(x + 3) = x² + 5x + 6

Problem 3

Factor the trinomial below $$ x^2 - 2x -3 $$

Step 1

Identify a, b and c in the trinomial $$ax^2 + bx + c$$

$$ a = 1 \\ \blue { b = -2} \\ \red { c= -3} $$

Step 2

Write down all factor pairs of $$ \red {-3 } $$ (yes, the negative sign matters!)

(Note: since c is negative, we only need to think about pairs that have 1 negative factor and 1 positive factor. Remember a negative times a positive is a negative)

Step 3

Identify which factor pair from the previous step sums up to $$ \blue { -2} $$

Step 4

Substitute that factor pair into two binomials

(x + 1)(x - 3)

Step 5

If you'd like, you can check your work by multiplying the two binomials and verify that you get the original trinomial

$$ (x + 2)(x - 3) = x^2 - 2x - 3 $$

Problem 4

Factor the trinomial below $$ x^2 - 5x + 6 $$

Step 1

Identify a, b and c in the trinomial $$ ax^2+ bx + c $$

$$ a = 1 \\ \blue{ b - 5} \\ \red{ c = 6} $$

Step 2

Write down the factor pairs of $$ \red 6 $$

(Note: since 6 is positive we only need to think about pairs that are either both positive or both negative. Remember a negative times a negative is a positive.)

Step 3

Identify which factor pair from the previous step sum up to $$ \blue{-5} $$

Step 4

Substitute that factor pair into two binomials .

$$ (x - 2)(x - 3) $$

Step 5

If you'd like, you can check your work by multiplying the two binomials and verify that you get the original trinomial

$$(x - 2)(x - 3) = x^2 - 5x + 6 $$

Problem 5

Factor the trinomial below $$ x^2 - 2x - 15$$

Step 1

Identify a, b and c in the trinomial $$ ax^2 + bx + c $$

$$ a = 1 \\ \blue{ b = -2 } \\ \red{ c = -15} $$

Step 2

Write down the factor pairs of $$ \red{ -15} $$ (Note: since c is negative we only need to think about pairs that have 1 negative factor and 1 positive factor. Remember a negative times a positive is a negative.)

Step 3

Identify which factor pair from the previous step sums up to $$ \blue{-2} $$

Step 4

Substitute that factor pair into two binomials

$$ (x + 3)(x - 5) $$

Step 5

If you'd like, you can check your work by multiplying the two binomials and verify that you get the original trinomial

$$ (x + 3)(x - 5) = x^2 - 2x - 15 $$

Factor Trinomial Worksheet

Factor Trinomial Calculator

How To Factor Trinomials

What is a Trinomial?

Solver

Video Tutorial of Factoring a Trinomial

Formula For Factoring Trinomials (when $$ a = 1 $$ )

Example of Factoring a Trinomial

Practice Problems

Problem 1

Problem 2

Problem 3

Problem 4

Problem 5

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com

$$ 3x^2 + 2x + 1$$
$$ 7x^2 + 4x + 4$$
$$5 x^2 + 6x + 9$$

$$ x^{\red 3} + 2x + 1 $$ this is not a quadratic trinomial because there is an exponent that is $$ \red { \text{ greater than 2} } $$
$$ 2x + 4 $$ this is not a quadratic trinomial because there is not exponent of 2. In fact, this is not even a trinomial because there are 2 terms
$$ 5x ^{\red 3} + 6x^2 + 9$$ this is not a quadratic trinomial because there is an exponent that is $$ \red { \text{ greater than 2} } $$