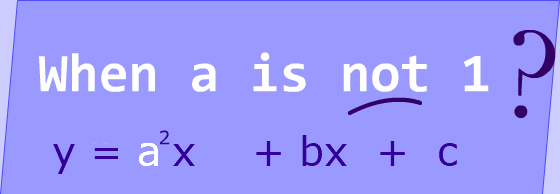Factor by Grouping : A Formula

To factor a polynomial you must reduce the polynomial expression to its factors.

We are going to use a method known as the 'ac' method to factor by grouping. Many people do not realize that there is actually a systematic way to factor by grouping. This is the closes thing to a 'formula' that you will find for factoring by grouping. It is always much easier to look at some example problems before reading generalized steps, but the steps go as follows

Formula for Factoring By Grouping

• Step 1) Determine the product of AC (the coefficients in a quadratic equation)
• Step 2) Determine what factors of AC sum to B.
• Step 3) "ungroup" the middle term to become the sum of the factors found in step 2
• Step 4) group the pairs.

As I expressed earlier, it's much easier to understand this method by simply walking through a few examples. So don't worry if the steps above seem like algebraic nonsense -- just check out the example problems below.

3x² +8x + 4
Product of (a)(c) = (3)(4) = 12
What factors of 12 sum to 8?

Answer

2 & 6
Think of 8x as 2x + 6x
3x² + 2x + 6x + 4
Group the 2 pairs : (3x² + 2x) + (6x + 4)
Remove the common factors:: x(3x + 2) + 2(3x + 2)
Rewrite as grouped factors: (x + 2)(3x + 1)

3x² + 7x + 4
Product of (a)(c) = (3)(4) = 12
What factors of 12 sum to 7?

Answer

Answer: 3 & 4
Think of 7x as 3x + 4x
3x² + 3x + 4x + 4
Group the 2 pairs : (3x² + 3x) + (4x + 4)
Remove the common factors: 3x(x + 1) + 4(x + 1)
Rewrite as grouped factors: (3x + 4)(x + 1)

5x² + 18x + 9

Show Factors By Grouping

Use the formula
Product of (a)(c) = (5)(9) = 45
What factors of 45 sum to 18?
Answer: 3 & 15
Think of 18x as 3x + 15x
5x² + 3x + 15x + 9
Group the 2 pairs : (5x² + 3x) + (15x + 9)
Remove the common factors: x(5x + 3) + 3(5x + 3)
Rewrite as grouped factors: (x + 3)(5x + 3)

2x² + 5x + 3

Factor it

Apply our formula
Product of (a)(c) = (2)(3) = 6
What factors of 6 add up to to 5?
Answer: 3 & 2
Think of 5x as 2x + 3x
2x² + 2x + 3x + 3
Group the 2 pairs : (2x² + 2x) + (3x + 3)
Remove the common factors: 2x(x + 1) + 3(x + 1)
Rewrite as grouped factors: (2x + 3)(x + 1)

5x² + 13x + 6

Factor By Grouping

Remember our formula
Product of (a)(c) = (5)(6) = 30
What factors of 30 add up to to 13?
Answer: 3 & 10
Think of 13x as 10x + 3x
5x² + 10x + 3x+ 6
Group the 2 pairs : (5x² + 10x) + (3x+ 6)
Remove the common factors: 5x(x + 2) + 3(x + 2)
Rewrite as grouped factors: (5x + 3)(x + 2)

7x² + 9x + 2

Factor By Grouping

You know the deal-- Use our formula for factoring by grouping
Product of (a)(c) = (7)(2) = 14
What factors of 14 add up to to 9?
Answer: 7 & 2
Think of 9x as 7x + 2x
7x² + 7x + 2x + 2
Group the 2 pairs : (7x² + 7x) + (2x + 2)
Remove the common factors: 7x(x + 1) + 2(x + 1)
Rewrite as grouped factors: (7x + 2)(x + 1)