Mathwarehouse Logo

Find Reference Angle

Unit Circle Game unit circle game
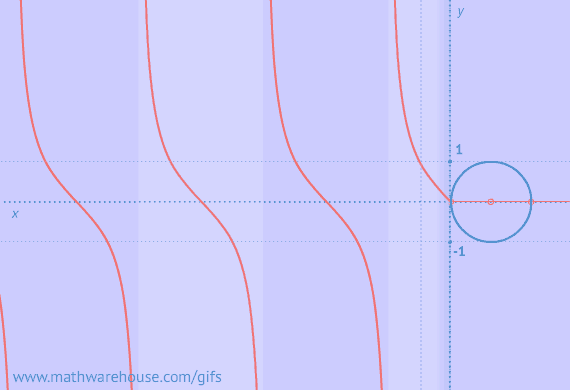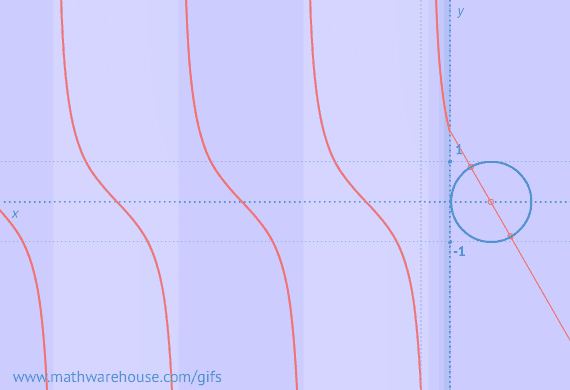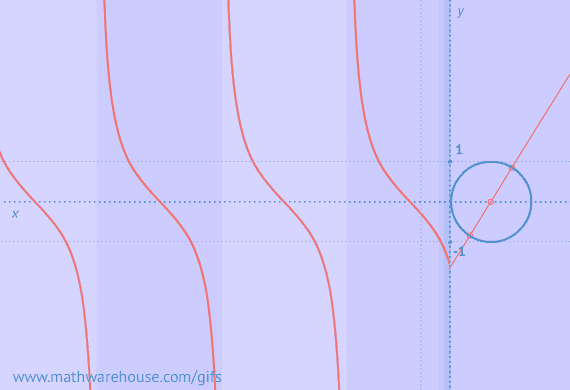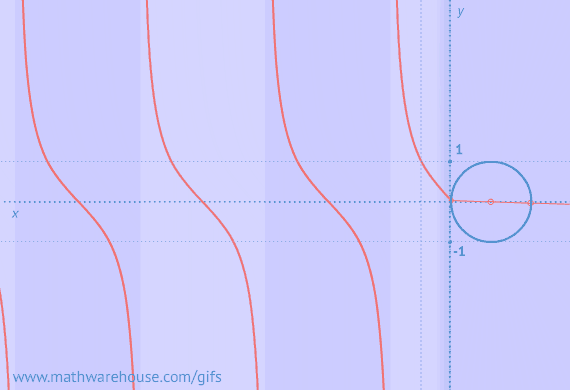
Trigonometry Gifs Graph of Cotangent

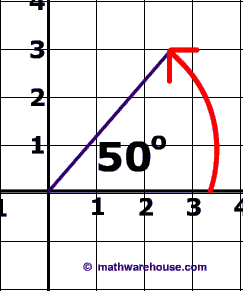
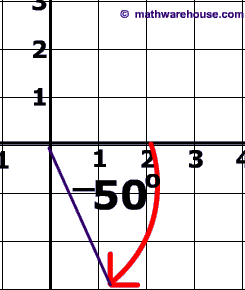
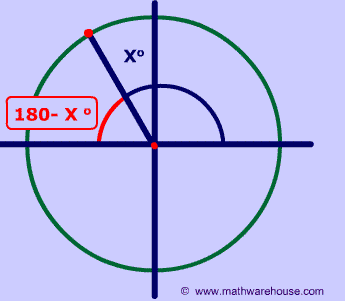
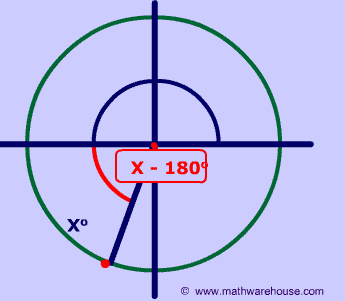
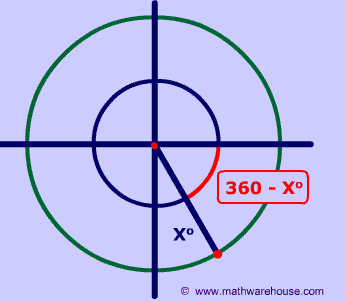
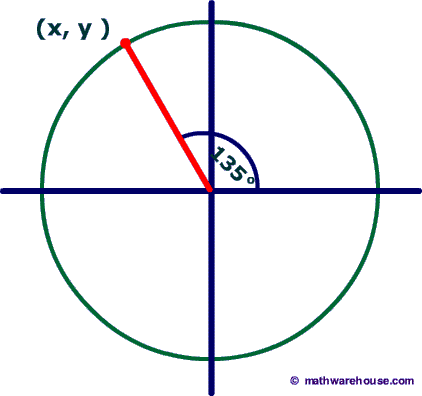
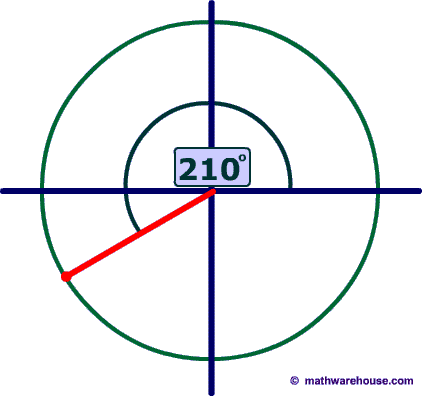
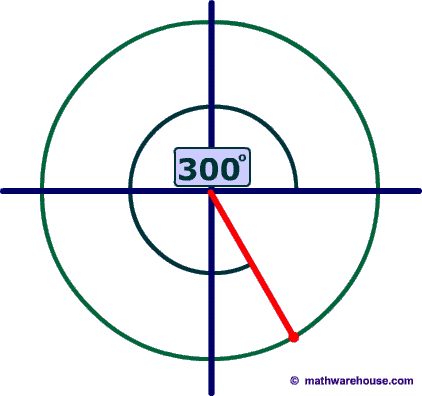
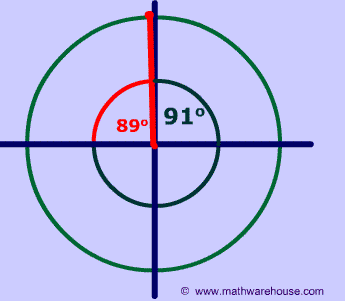
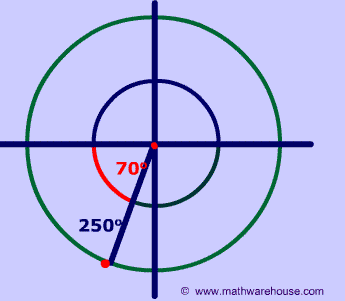
The reference angle is the positive acute angle that can represent an angle of any measure.

The reference angle $$ \text{ must be } < 90^{\circ} $$.

In radian measure, the reference angle $$\text{ must be } < \frac{\pi}{2} $$.

Basically, any angle on the x-y plane has a reference angle, which is always between 0 and 90 degrees. The reference angle is always the smallest angle that you can make from the terminal side of an angle (ie where the angle ends) with the x-axis. A reference angle always uses the x-axis as its frame of reference.

Rules of Angles and Reference angle

Positive angles go in a counter clockwise direction. Below is a picture of a positive fifty degree angle.

positive reference angle
negative reference angle

Quadrant I

Every positive angle in quadrant I is already acute...so the reference angle is the measure of the angle itself:

Quadrant II

To find the reference angle measuring x ° for angle in Quadrant II, the formula is $$ 180 - x^{\circ} $$.

quadrant II general pic

Quadrant III

To find the reference angle measuring x ° for angle in Quadrant III, the formula is $$ x - 180 ^{\circ} $$.

quadrant II general pic

Quadrant IV

To find the reference angle measuring x ° for angle in Quadrant IV, the formula is $$360 ^{\circ} -x $$.

quadrant II general pic

Practice Problem

Problem 1

What is the reference angle for the angle in the graph below?

problem 1

Remember that the reference angle always uses the x-axis as a frame of reference.

Problem 2

What is the reference angle for a 210° angle?

problem 2

Remember that the reference angle always uses the x-axis as a frame of reference.

Problem 3

What is the reference angle for a 300° angle?

problem 3

Remember that the reference angle always uses the x-axis as a frame of reference.

Word Problems

Problem 4

What is the reference angle for an angle that measures 91°?

For a quadrant 2 angle, the reference angle is always 180° - given angle.

In this case, $$ 180 - 91 = \color{Red}{89} $$.

91 degree reference angle
Problem 5

What is the reference angle for an angle that measures 250°?

For a quadrant 3 angle, the reference angle is always given angle - 180°.

In this case, $$ 250 - 180= \color{Red}{ 70 } $$.

91 degree reference angle
Unit Circle Game unit circle game
Trigonometry Gifs Graph of Cotangent
Further Reading:
Back to Trigonometry Next to Unit Circle Game

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!