Graph of Cotangent from Unit circle
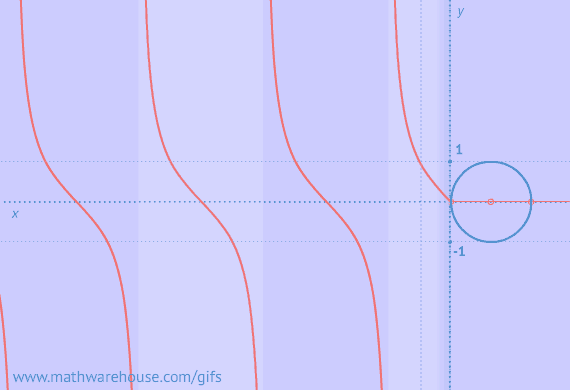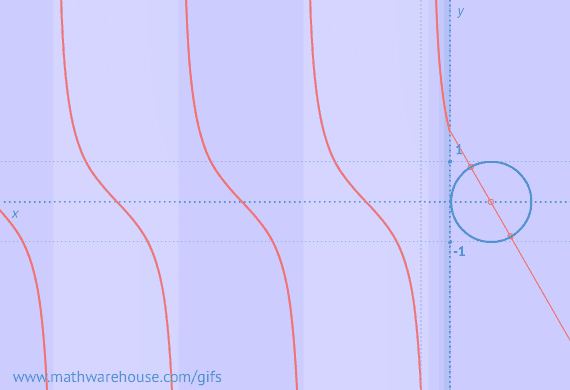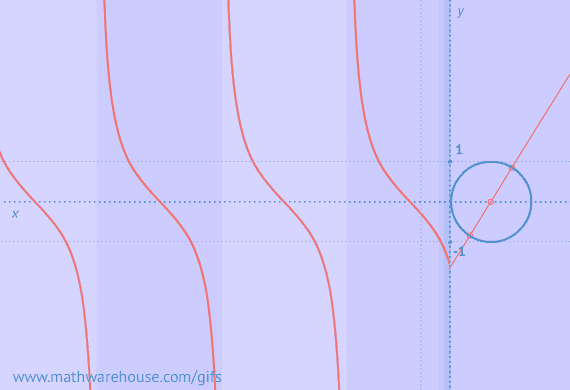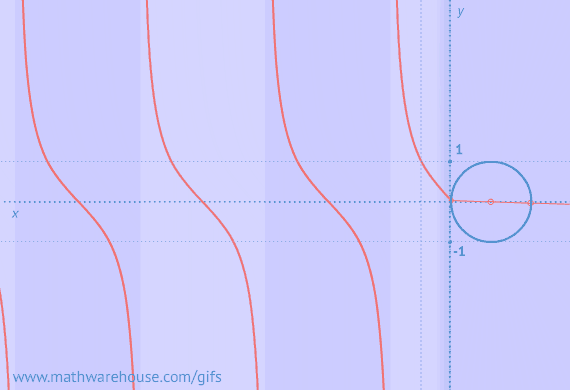
Graphs of Sine/Cosine From Unit Circlle
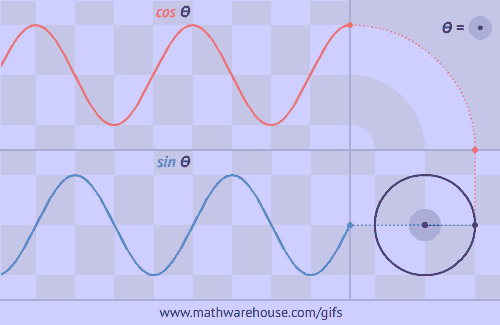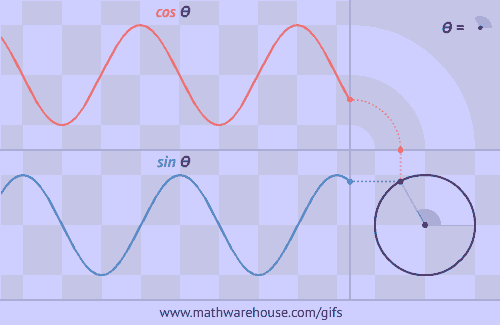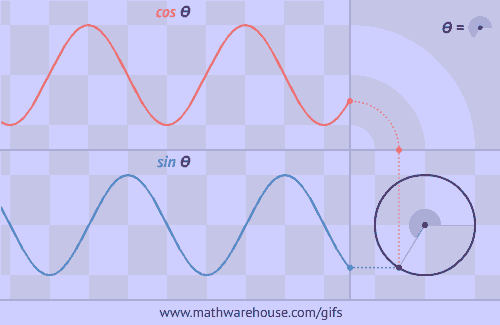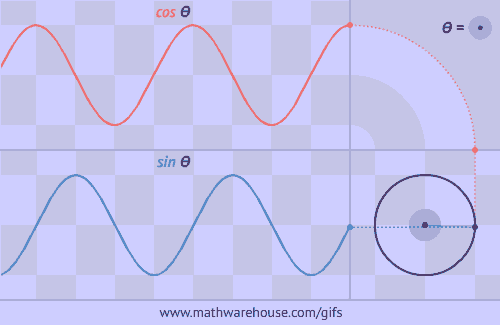
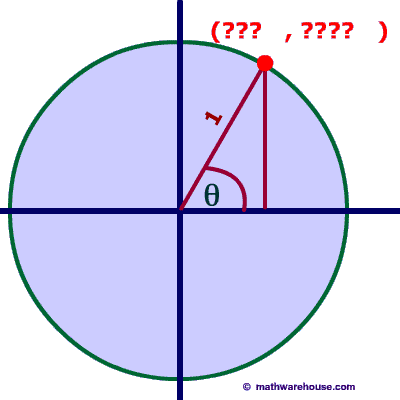
The Unit Circle is a circle with a radius of 1. The angle that we rotate the radius uses the greek letter θ.
Formula for the Unit Circle
The formula for the unit circle relates the coordinates of any point on the unit circle to sine and cosine. According to the formula, the x coordinate of a point on the unit circle is $$cos (\theta)$$ and the y coordinate of a point on the unit circle is $$ sin(\theta)$$ where Θ represents the measure of an angle that goes counter clockwise from the positive x-axis. This formula is much easier to see and understand from a picture. See the first problem below.
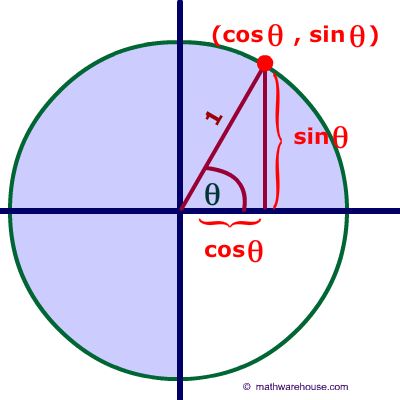
Demonstration of Unit Circle's Formula
Practice Problems
Problem 1
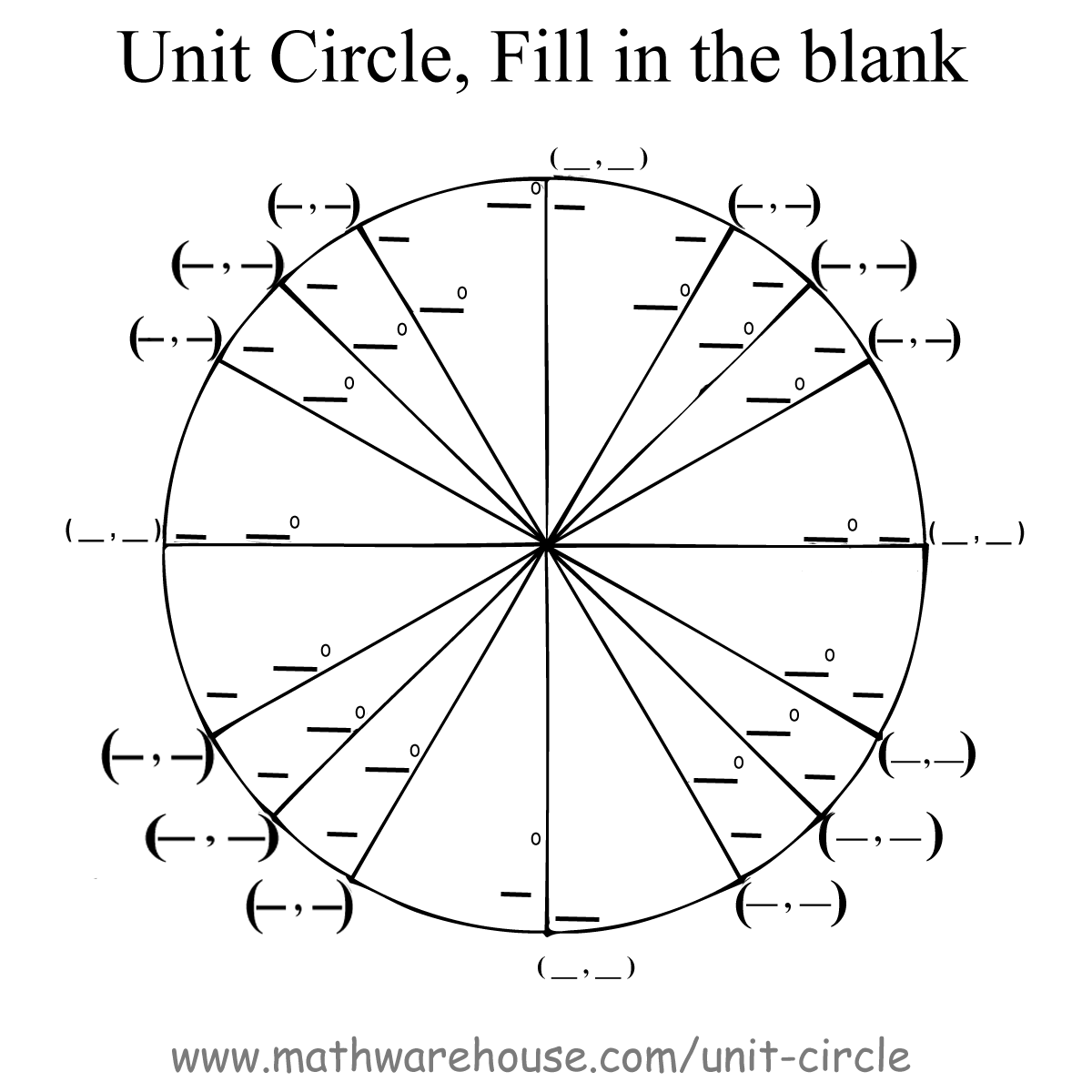
Problem 2
The value of the x coordinate is the $$ cos(\theta)$$ and the y coordinate is $$ sin(\theta)$$.
Problem 3
Remember the formula for the unit circle. Cosine represents the x value, segment AB, sine represents the y value or CB and the tangent line rests outside the circle and is DF.
Problem 4
Remember the formula for the unit circle. Cosine represents the x value, segment AB, sine represents the y value or CB and the tangent line rests outside the circle and is DF.
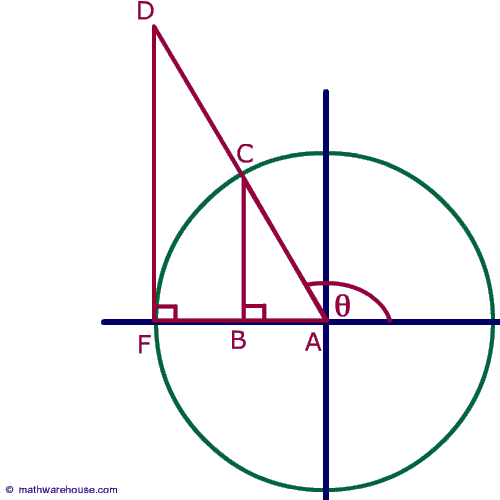
Problem 5
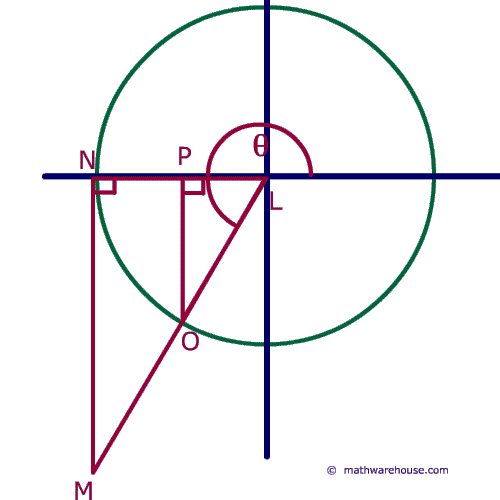
Remember the formula for the unit circle. Cosine represents the x value, segment PL, sine represents the y value or PO and the tangent line rests outside the circle and is NM.
Problem 6
Remember the formula for the unit circle. Cosine represents the x value, segment AE, sine represents the y value or ED and the tangent line rests outside the circle and is BC.
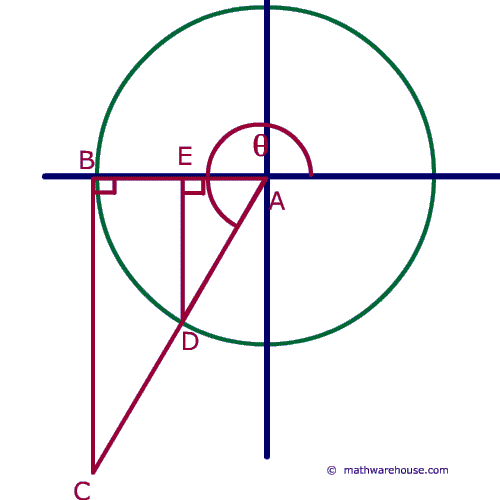
Problem 7
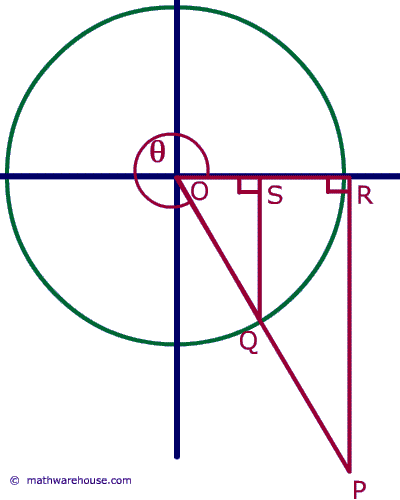
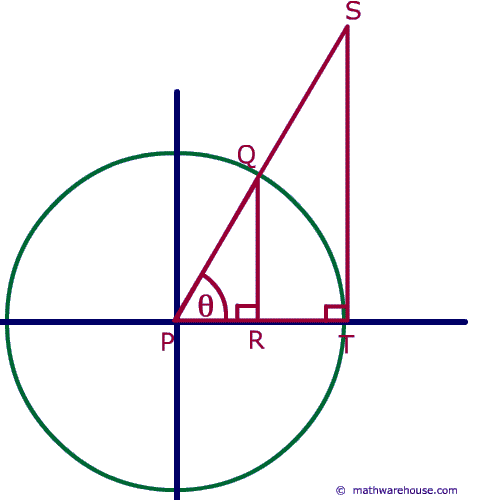
Remember the formula for the unit circle. Cosine represents the x value, segment OS, sine represents the y value or SQ and the tangent line rests outside the circle and is PR.