Formula and laws of logarithms
-
Product rule: logbAC = logbA + logbC
- Ex: log464 = log44 + log416 = log4(4•16)
- practice problems on the product rule
-
Quotient rule: logb(A/C) = logbA − logbC
-
Ex: $$ log_3(\frac{27}{9}) = log_3(27) - log_3(9) = 3-2 =1 $$
practice problems on the quotient rule
-
Ex: $$ log_3(\frac{27}{9}) = log_3(27) - log_3(9) = 3-2 =1 $$
-
Power rule: logbAC = C(logbA)
- Ex: log39² = 2log39
Practice problems on the power rule
- Ex: log39² = 2log39
Product Rule Practice Problems
log12 + log5 = log(12*5) = log60
log312 + log311 = log3(12 *11) = log3132
log511 + log5a = log5(11*a) = log511a
Quotient Rule Practice Problems
$ log20 -log5 = log(\frac{20}{5}) = log4 $
$ log_2(100) -log_2(25) = log_2(\frac{100}{25}) = log_2(4). $
log24 is a logarithm equation that you can solve and get an answer of 2
$ log_2(40) - log_2(5) = log_2(\frac{40}{5}) = log_2(8). $
log28 is a logarithm equation that you can solve and get an answer of 3
$ log_3(18) - log_3(2) = log_3(\frac{18}{2}) = log_3(9). $
log39 is a logarithm equation that you can solve and get an answer of 2
Power Rule Practice Problems
log3x2= 2log3X
log39x= xlog39
log39 can be solved as a logarithmic equation. log39 = 2Therefore, the final answer is x(2) or 2x
Practice Problems:
all rules and formulas
Problem 1
If log x = 4 and log y =2 what is the numeric value of 
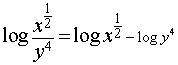Now, apply the quotient rule and then the power rule
After applying these rule of logarithms , substitute in the value of log x and log y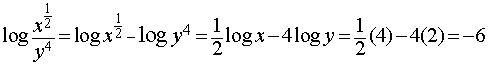 
-
Practice Problems:
- product rule practice
- quotient rule practice
- power rule practice
