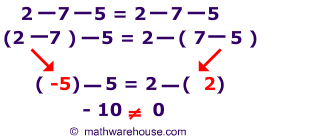Definition: The associative property states that you can add or multiply regardless of how the numbers are grouped. By 'grouped' we mean 'how you use parenthesis'. In other words, if you are adding or multiplying it does not matter where you put the parenthesis. Add some parenthesis any where you like!.
Examplesof the Associative Property for Addition
The picture below illustrates that it does not matter whether or not we add the 2 + 7 first (like the left side) or the 7 + 5 first, like the right side.
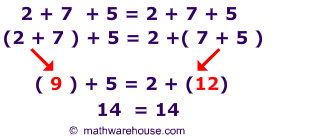
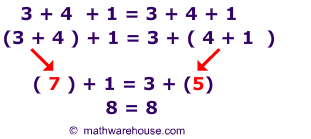
(a + b) + c = a + (b + c) – Yes, algebraic expressions are also associative for addition
Examplesof the Associative Property for Multiplication
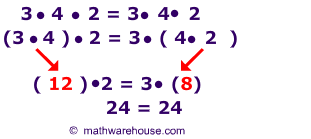
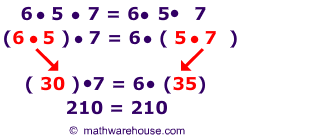
(a • b) •c = (a • b) •c – Yes, algebraic expressions are also associative for multiplication
Non Examples of the Associative Property
Division (Not associative)
Division is probably an example that you know, intuitively, is not associative. The examples below should help you see how division is not associative.
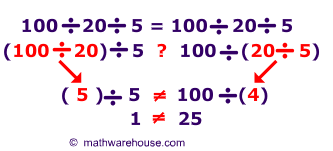
Subtraction(Not associative)
Subtraction is also not associative..
